作者简介: 李河(1963#cod#x02013;),男,内蒙古商都人,主任医师,医学博士, 主要研究方向为流行病学与医学统计学在临床医学科研中应用、心血管病的二级预防研究。
在临床医学科研中常会遇到生存数据的统计学处理分析问题,而比例危险率回归模型(简称COX回归模型)常用来进行影响生存时间的多因素分析;故在论文撰写中需根据科研设计类型和研究变量特征,进行合理的临床流行病学和医学统计学思维,以便得到正确结果。
It’s a common situation for a survival data statistics in the clinical researches. Proportional hazards regression model is often applied for the multivariate analysis on survival time. So, it’s necessary to have a correct thinking in clinical epidemiology and medical statistics for the good paper-writing, which is based on the research-type and variable-characteristic, as to achieve a correct result.
在临床医学科研中常常会遇到如下生存研究数据, 如心脏瓣膜置换术后瓣膜存活时间研究、肿瘤病人接受治疗后其生存时间研究等。生存数据(寿命数据)可分为完全数据和截尾数据。完全数据如当病人确诊为某病(或开始治疗)到病人死亡(或到治愈)为止所经历的全部时间。截尾数据(或删失数据)中, 左截尾数据为记录之前的某个时刻发生了终点事件(如死亡)但确切发生(死亡)时间未知; 右截尾数据为记录之后仍存活但确切发生终点事件(死亡)的时间未知; 区间截尾数据为某个时间区间发生了终点事件(如死亡)但确切发生(死亡)时间未知。生存分析是需要同时考虑生存结果和生存时间的一种统计学方法, 可以充分利用截尾数据的信息, 对生存时间分布特征及生存时间的主要影响因素进行分析。医学统计学中处理分析生存数据的统计学方法可简单划分为:参数分析法(如指数分布、威布尔分布)、非参数分析法(寿命表法、KAPLAN-MEIER乘积极限法)、半参数分析法(COX回归模型)。本文以下列模拟数据为例来说明COX回归模型在临床医学科研中的应用价值。
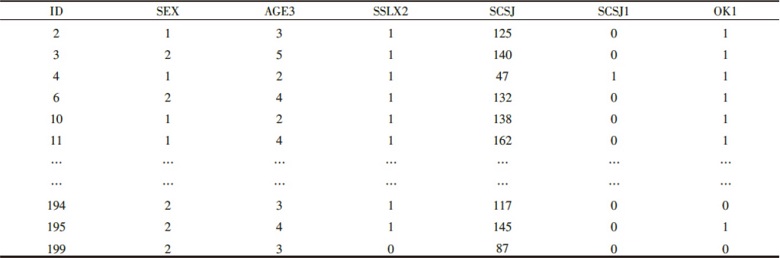
以接受心脏瓣膜置换术后病人随访数据库(aa1.sas7bdat)为基础, 截取其中128例研究对象的相关变量数据为例, 并且对有关数据进行变量变换, 来举例分析说明瓣膜置换术后瓣膜的生存状况。用于本例的数据中, 研究对象男60例、女68例, 年龄7~51岁, 平均年龄及标准差29.33± 9.32岁, 其中二尖瓣置换术121例, 非二尖瓣置换术7例, 对研究对象的平均随访时间为92.3个月(5~219个月)。本例数据相关研究变量定义如下:编号ID为研究对象统一编号, 性别SEX(男性=1, 女性=2), 年龄AGE3(从小到大每10岁为一年龄等级), 手术类型SSLX2(二尖瓣置换术=1, 非二尖瓣置换术=0), 瓣膜生存时间SCSJ(实际生存时间), 终点事件SCSJ1(终点事件SCSJ1=1为发生瓣膜生存时间小于5年事件、否则SCSJ1=0), OK1(完全数据OK1=1, 截尾数据OK1=0), 见表1。
| 表1 心脏瓣膜置换术后瓣膜生存状况数据 |
为了分析性别、年龄及手术类型对瓣膜生存状况的影响, 甲医生对上述生存数据进行了如下统计学处理分析:首先依据上数据库定义相关协变量为性别SEX(男性=1, 女性=2), 年龄AGE3(从小到大每10岁为一年龄等级), 手术类型SSLX2(二尖瓣置换术=1, 非二尖瓣置换术=0); 定义因变量为“ 瓣膜生存时间小于5年即为发生终点事件, 并且赋值SCSJ1=1, 反之赋值SCSJ1=0” , 然后运行SAS程序执行二分类因变量的多变量Logistic回归分析、二分类因变量的多变量逐步Logistic回归分析(取协变量引入方程的检验水准α = 0.05, 剔出方程的检验水准α =0.10), 表2结果显示年龄每增加一个等级(增加10岁), 发生瓣膜生存时间小于5年(发生终点事件)的比数比(odds ratios, OR)=0.456(95%可信区间0.287~ 0.725), 差异有统计学意义(χ 2=10.989 3, P=0.000 9); 而性别及手术类型对瓣膜生存时间的影响无统计学意义(χ 2=0.896 6, P=0.343 7; χ 2=0.669 2, P=0.413 3)。表3结果显示年龄每增加一个等级(增加10岁), 发生瓣膜生存时间小于5年(发生终点事件)的比数比OR=0.482(95%可信区间0.306~0.759), 差异有统计学意义(χ 2=9.924 2, P=0.001 6)。SAS参考程序及结果如下[1, 2, 3]:
data aa.aa2; set aa.aa1;
if id='.' then delete;
if scsj='.' then delete;
if scsj< =60 then scsj1=1;
else if scsj> 60 then scsj1=0;
if id > 200 then delete; run;
ods rtf;
proc logistic data=aa.aa2 descending;
model scsj1=sex age3 sslx2;
run; ods rtf close;
ods rtf;
proc logistic data=aa.aa2 descending;
model scsj1=sex age3 sslx2/selection=stepwise sle=0.05 sls=0.10; run;
ods rtf close;
而乙医生对上述数据进行了如下处理:为了分析性别、年龄及手术类型对瓣膜生存状况的影响, 定义相关协变量为性别SEX(男性=1, 女性=2), 年龄AGE3(从小到大每10岁为一年龄等级), 手术类型SSLX2(二尖瓣置换术=1, 非二尖瓣置换术=0); 因变量取瓣膜生存时间SCSJ(生存时间), 并且定义其数据特性变量OK1(完全数据赋值OK1=1, 截尾数据赋值OK1=0)。然后进行多变量COX回归分析、多变量逐步COX回归分析(协变量引入方程的检验水准α =0.05, 剔出方程的检验水准α =0.10), 表4结果显示性别、年龄及手术类型对瓣膜生存时间的影响皆未见差异有统计学意义(χ 2=0.416 6, P=0.518 6; χ 2=1.738 3, P=0.187 4; χ 2=0.692 7, P=0.405 2)。表5结果显示在检验水准取α =0.05时, 进行多变量逐步COX回归分析未见协变量引入方程(NOTE: No (additional) variables met the 0.05 level for entry into the model.)。SAS参考程序及结果如下[3, 4]:
data aa.aa2;
set aa.aa1;
if id='.' then delete;
if scsj='.' then delete;
if id > 220 then delete;
run;
ods rtf;
proc phreg data=aa.aa2;
model scsj∗OK1(0)=sex age3 sslx2/RL; run;
ods rtf close;
ods rtf;
proc phreg data=aa.aa2;
model scsj∗OK1(0)=sex age3 sslx2/RL selection=stepwise sle=0.05 sls=0.10; run;
ods rtf close;
由上可见, 甲医生采用二分类因变量多变量Logistic回归分析、二分类因变量多变量逐步Logistic回归分析(取协变量引入方程的检验水准α =0.05, 剔出方程的检验水准α =0.10)的统计学结果, 与乙医生采用多变量COX回归分析、及多变量逐步COX回归分析(协变量引入方程的检验水准α =0.05, 剔出方程的检验水准α =0.10)的结果不同, 甲乙两医生何者在医学统计学思维上科学合理?
| 表2 瓣膜生存时间5年影响生物瓣膜生存的危险因素Logistic回归分析 |
| 表3 瓣膜生存时间5 年影响生物瓣膜生存的危险因素逐步Logistic 回归分析 |
| 表4 影响生物瓣膜生存时间危险因素COX回归分析 |
| 表5 影响生物瓣膜生存时间危险因素逐步COX回归分析 |
从科学合理的统计学思维来分析, 乙医生对本例资料的统计学处理分析是恰当的, 而甲医生的统计学处理分析存在错误。因为生存分析的因变量是终点事件结局及出现该终点事件结局所经历的时间大小。生存数据常常不满足正态分布要求、不满足一般多变量线性回归模型的要求, 故以生存时间为因变量建立一般多变量线性回归模型不妥。而以某一时点的终点事件结局(如1=发生终点事件, 0=未发生终点事件)为因变量, 进行二分类因变量多变量Logistic回归分析, 则没有充分利用生存时间大小的信息, 也没有考虑生存时间数据还存在的数据删失问题, 故二分类因变量多变量Logistic回归模型也不适合分析此类数据。而且一般多变量线性回归模型模型和二分类因变量多变量Logistic回归模型都无法充分利用这类删失数据提供的信息。
故在进行生存数据统计学处理分析、进行影响生存时间大小的多因素分析时, 应该采用比例危险率回归模型(COX回归模型)。这也要求我们在临床医学科研实际工作或论文撰写过程中, 需要根据科学研究设计类型(包含专业研究设计和统计研究设计)及所收集数据研究变量的特征, 进行科学合理的临床流行病学思维、医学统计学思维, 运行国际上承认统计分析软件(如SAS), 得出正确的统计学结果[5]。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|