从理论上讲, 估计样本含量的原则是在保证“ 研究结果” 具有一定可信度（1-α ）（或可信区间）及把握度（1-β ）的前提下求得所需要的“ 研究对象的最小例数” , 以便通过对样本研究来推断总体, 如果考虑到失访（或丢失）可以据不同情况可以增加10%~20%的样本量。样本含量太大, 往往导致人力、物力、财力、时间上的浪费, 而且由于盲目追求样本数量常可能导致更多混杂因素（confounding factor）的发生, 导致更大的偏倚（bias）发生。样本含量太小, 常导致检验效能（把握度1-β ）降低, 导致假阴性结果出现。决定“ 样本含量” 的基本因素有：（1）检验水准α （可信区间, 需要区分单侧或双侧）; （2）检验效能 1-β （把握度, 为单侧）; （3）总体参数, 如总体均数μ 、总体率π 的估计值（或目标值）, 或总体变异度σ 、σ ²的估计值（总体方差或变异度）; （4）有意义的δ 的估计值（δ 为容许误差, 可以是绝对容许误差或相对容许误差）。有时还需要考虑实验设计类型的要求。

检验效能或称把握度（power of a test）是指如果对比组间的某“ 总体指标” 确实存在有实际意义的差异, 采用现有统计学假设检验能够有效发现这种差异的能力。检验效能取决于第二类错误概率β 的大小, 即power=1-β 。当假设检验结果为P> 0.05, 即出现“ 阴性” 统计学结果时, 就需要提供检验效能或把握度的大小, 以便能够正确理解假设检验出现“ 阴性” 统计学结果的正确性。实际工作中可以采用统计学软件（如statistical analysis system, SAS）来估算检验效能（power=1-β ）的大小。如果检验效能偏小, 可能由于样本含量不够大, 需要进一步增加样本含量; 如果检验效能足够大, 这时可以接受假设检验为“ 阴性” 的统计学结果, 即“ 接受H₀” , 可以认为本次抽样研究的统计学结果为对比组间的某“ 总体指标” 差异未见统计学意义; 此时犯第二类错误概率β 的大小在可以接受范围内（如β ≤ 0.10）。

对于两生存率比较的样本含量估计及检验效能估算, 可以根据研究设计类型区分为双侧检验与单侧检验。我们可以应用计算机运行统计学软件（如SAS）来完成样本含量估计, 供读者参考。例如：拟进行一项临床试验研究, 比较一新药（B药）与标准药（A药）的抗肺癌疗效, 据文献使用标准药（A药）治疗肺癌病例的3年生存率为45%, 现研究者据前期预试验结果估计使用新药（B药）治疗肺癌病例的3年生存率落在60%, 如果整个临床试验期设定为5年, 而研究病例招募工作要在临床试验的前2年内完成, 那么发现此种差异具有统计学意义至少需要多大样本量?并对其相应的检验效能进行估算?

SAS参考程序及结果如下：

OPTIONS NOCENTER;

TITLE ˑ ‘ 两生存率比较的样本含量估计（双侧检验）与检验效能估算‘ ;

ODS RTF;

PROC POWER;

TwoSampleSurvival test = logrank

Curve（"Group_A"） = 3 ∶ 0.45

Curve（"Group_B"） = 3 ∶ 0.60

GroupSurvival = "Group_A" | "Group_B"

Accrualtime = 2

Followuptime = 5

Npergroup = .

alpha = 0.05

sides = 2 /∗ 双侧检验 ∗/

Power = 0.75 0.80 0.85 0.90;

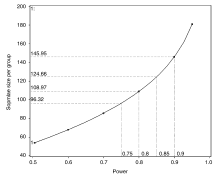
Plot X= Power min= 0.5 max= 0.95 key=bycurve（pos = inset numbers = on）

Xopts = （ref = 0.75 0.80 0.85 0.90 crossref =yes）

markers = nice;

RUN; ODS RTF CLOSE;

计算所得不同把握度对应的样本含量见表1和图1。

表1

表1

表1 不同把握度对应的样本含量 Computed N Per Group Index Nominal Power Actual Power N Per Group 1 0.75 0.753 97 2 0.80 0.800 109 3 0.85 0.851 125 4 0.90 0.900 146

表1 不同把握度对应的样本含量

图1

	Figure Option ViewDownloadNew Window
	图1 每组所需要样本例数

由结果可知, 据现有资料A药3年生存率为45%、B药3年生存率为60%, 如取α =0.05（双侧）、β =0.10（即把握度1-β =90%）时, 设计整个临床试验期为5年, 前2年内完成研究病例招募, 则进行两生存率比较的样本含量为每组需要样本例数146例（N Per Group=146）。如果取α =0.05（双侧）, 分别取β =0.10、0.15、0.20、0.25（即把握度1-β 分别取0.90、0.85、0.80、0.75）时, 进行两生存率比较的样本含量为每组需要样本例数分别为146例、125例、109例、97例。可见在取α =0.05（双侧）时, 随着把握度（1-β ）的逐步降低, 对应的每组样本例数（n per group）在逐步减少, 可见把握度越低需要随机抽样的样本含量越小。

可见, 在研究设计阶段, 如取α =0.05（双侧检验）, 要求β =0.10时（即把握度1-β =90%）时, 进行两生存率比较的样本含量为每组为146例（两组为292例）。在对主要研究指标“ 3年生存率” 进行统计学假设检验时, 如检验结果为P< 0.05, 即出现“ 阳性” 统计学结果时, 则“ 拒绝H₀” , 可以认为“ A药3年生存率与B药3年生存率” 差异有统计学意义, 此时可能犯第一类错误（假阳性）的概率为α ≤ 0.05。

如果假设检验结果为P> 0.05, 即出现“ 阴性” 统计学结果时, 即“ 不拒绝H₀” , 此时就需要提供检验效能或把握度（1-β ）的大小, 以便能够正确理解假设检验出现“ 阴性” 统计学结果的正确性。如果检验效能偏小, 可能由于样本含量不够大, 需要进一步增加样本含量, 才有可能正确发现（或判断）“ A药3年生存率与B药3年生存率” 是否真正存在差异。如果检验效能足够大（如大于0.90）, 这时可以接受假设检验为“ 阴性” 即“ 不拒绝H₀” , 的统计学结果, 可以认为本次抽样研究的统计学结果为“ A药3年生存率与B药3年生存率” 差异未见统计学意义; 此时可能犯第二类错误（假阴性）的概率为β , 其大小是在可以接受范围内（如β ≤ 0.10）。

SAS参考程序及结果如下：

OPTIONS NOCENTER;

TITLE ˑ ’ 两生存率比较的样本含量估计（双侧检验）与检验效能估算’ ˑ ;

ODS RTF;

PROC POWER;

TwoSampleSurvival test=logrank

Curve（"Group_A"） = 3 ∶ 0.45

Curve（"Group_B"） = 3 ∶ 0.60

GroupSurvival = "Group_A" | "Group_B"

Accrualtime = 2

Followuptime = 5

Power = .

alpha = 0.05

sides= 2 /∗ 双 侧 检 验 ∗/

Npergroup= 100 to 160 by 10;

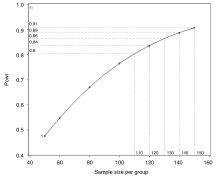
Plot X= N min = 50 max = 150 key= bycurve（pos = inset numbers = on）

Xopts= （ref = 110 120 130 140 150 crossref =yes）

markers = nice;

RUN; ODS RTF CLOSE;

计算所得不同样本含量对应的把握度见表2和图2。

图2

	Figure Option ViewDownloadNew Window
	图2 不同样本含量对应的把握度

表2

表2

表2 不同样本含量对应的把握度 Computed Power Index N Per Group Power 1 100 0.766 2 110 0.804 3 120 0.837 4 130 0.865 5 140 0.888 6 150 0.908 7 160 0.925

表2 不同样本含量对应的把握度

由结果可知, 据现有资料进行两生存率比较的样本含量估计（双侧检验）与检验效能估算, 如果每组样本含量分别取110、120、130、140、150时（n per group=110、120、130、140、150）, 对应的检验效能或把握度（1-β ）分别为0.804、0.837、0.865、0.888、0.908。

可见, 在取α =0.05（双侧检验）, 随着每组样本例数（N Per Group）的增多对应的把握度在逐步增高, 也即样本含量越小把握度就越低。当在每组样本含量取110时, “ 现有数据” 难以得出在α =0.05（双侧检验）、β =0.10（即把握度1-β =90%）的水平上“ A药3年生存率与B药3年生存率” 差异有统计学意义的结果。如果在每组样本含量取110时, 假设检验结果为P> 0.05, 即出现“ 阴性” 统计学结果时, 此时就需要提供检验效能或把握度（1-β ）的大小。由表2、图2可见, 在样本含量取110时, 把握度（1-β ）仅为0.804, 即如果对比组间的“ A药3年生存率与B药3年生存率” 确实存在有实际意义的差异, 在每组样本含量取110时, 采用现有统计学假设检验能够有效发现这种差异的能力仅为1-β =80.4%。

我们知道, 高质量的科学研究从研究设计阶段开始, 就需要生物统计学工作者参加, 并且需要自始至终的参加。因为统计设计对于保证研究结果的“ 重现性、可靠性、科学性” 具有非常重要的意义。而科研设计又包含专业设计和统计设计两部分内容。统计设计是对资料搜集、整理、分析全部过程的合理安排, 其主要内容有研究设计类型选择、研究对象选择（抽样随机化）、样本大小估计、研究对象分配（如随机化分组）、对照组设置、试验因素安排（如实验顺序安排随机化）、确定研究变量及相应统计分析方法等。不同的专业设计和统计设计所对应的样本含量（sample-size）与检验效能估算问题不同, 对应的统计学处理分析方法不同。有兴趣的读者可以进一步参阅专业书刊。