在医学科研中, 只要是抽样研究, 无论是实验设计还是调查设计均应考虑样本含量的估计^[1]。在以下两种抽样研究的情形下需要实施样本含量的估计：一是估计总体参数时, 二是进行假设检验时。在本文中, 我们将主要讨论假设检验时样本含量估计的问题, 而讨论后得出的结论则同样适用于估计总体参数时的样本量计算。以两个样本的t检验为例, 影响假设检验时样本含量估计的因素有四个：（1）第一类错误概率的大小α ：通常取α =0.05, 同时应明确是单侧检验还是双侧检验, α 定得越小, 所需的样本含量越大; （2）检验功效（1-β ）或第二类错误概率的大小β ：要求的检验功效越大, 所需的样本含量越大; （3）容许误差δ ：是假设检验试图揭示的差异大小, δ 越小, 所需样本含量越大; （4）总体标准差σ ：体现个体变异度的σ 越大, 所需样本量越大。根据已知条件所估计的样本量进行实验, 就意味着如果总体参数间确实存在δ 大小的差异, 则按照α 的检验水准, 有1-β 的概率得出差异具有统计学意义的结论。

若研究者无法得到总体参数间的差值δ , 一种说法是可通过预实验的组间差距作为容许误差δ , 另一种说法是可根据专业知识由各专业的专家确定有专业意义的差值作为容许误差δ , 如平均舒张期血压的差值> 0.69 kPa, 白细胞的平均差值0.5× 10⁹/L等, 第三种说法是对于没有给定专业意义上的容许误差水平的情况下, 用0.25倍或0.50倍的标准差来设定容许误差^[2]。对于以上三种做法, 究竟哪一种更适合用于样本量的估计?本文将结合实例来探讨δ 该取值方法。

以单样本均数检验或均数的配对检验为例, 样本量计算公式如下：

N=[(tα+tβ)Sδ]2（1）, 此式适合单侧检验

N=[(tα/2+tβ)Sδ]2（2）, 此式适合双侧检验

例 为了解高温作业工人的心率是否高于一般人群。某研究者随机抽取了10名高温作业工人做预实验, 测得其心率标准差S=6.2次/分。如设α = 0.05、β = 0.10时, 需要多大样本含量?

讨论一： 专业上认为高温作业工人的心率高于一般人群3.0次/分才有专业意义, 即δ _专 = 3.0次/分, 同时通过预实验可以得到δ _预, 现α =0.05, β =0.10, 均取单侧, 查表得t_{α , ∞} = t_{0.05, ∞} = 1.645, t_{β , ∞} = t_{0.10, ∞} = 1.282。

情况1：若δ _预 =2.4次/分< δ _专, 由公式（1）N = N=[(tα+tβ)Sδ]2知, N_预 = 58 > N_专 = 37, 同样由公式可知样本量越大, 越倾向于发现更小的差异, 即如果开始就按照N_预来进行实验, 会可以发现δ _预=2.4次/分的差异, 而这么小差异在专业上来说可以看作是“ 居于相同水平” 的。按照N_专进行正式研究, 将不能发现δ _预= 2.4次/分大小的差异, 但是, 这个阴性结果（差异无统计学意义）不被视作假阴性, 原因是专业上认为δ _专=3.0次/分以下的差异可视作心率水平一样, 采用δ _预计算出来的样本量会无谓地增加研究成本。

情况2：若δ _预= 5.2次/分 > δ _专, 由公式（1）知, N_预 = 13 < N_专= 37, 根据情况1的分析可知按照N_专 = 37进行实验会倾向于发现δ _专 = 3.0次/分的差异, 但是因为抽样误差的存在, 按照N_预 = 13进行实验也有可能得出阳性结果（差异有统计学意义）, 为避免成本浪费, 可先按照N_预进行正式研究（理论上可以发现δ _预= 5.2次/分的差异）, 根据研究结果判断是否需要追加样本量, 此时又会得到一个容许误差即δ _正, 存在以下三种可能性：

（1）δ _正 = 6.7次/分 > δ _预, 结果发现了更大的差异, 可视为阳性结果, 说明基于δ _预计算的样本量N_预= 13是充分的。

（2）δ _正 = 2.5次/分 < δ _专, 结果发现的差异只有2.5次/分, 视为阴性结果, 为了发现δ _专 = 3.0次/分的差异, 有必要追加样本量, 由公式（1）知N_专 = 37 < N_正= 53, 故此时样本量应该追加至37。

（3）δ _预 > δ _正= 4.3次/分 > δ _专, 结果发现的差异只有4.3次/分, 说明预实验的样本量不足, 于是把此次正式实验作为一次新的预实验, 根据δ _正 = 4.3次/分计算出样本量N_正 = 18, 因为抽样误差的存在, 可以认为按照N_正进行实验也有可能发现δ _专 = 3.0次/分的差异, 为避免浪费, 不妨先追加样本量至18（理论上可以发现δ _正 = 4.3次/分的差异）。根据实验结果判断样本量是否已足够, 追加样本量后进行实验会得到新的δ ′ _正, 进一步讨论如下：如果δ ′ _正 = 4.6次/分 > δ _正, 说明用基于样本量N_正 = 18进行实验结果发现了更大的差异, 可视为阳性结果, 说明当前样本量已充分, 可结束样本量的估计; 如果δ _专 < δ ′ _正 = 3.8次/分 < δ _正, 根据δ ′ _正 = 3.8次/分计算出样本量N′ _正 = 23, 同样因为抽样误差的存在, 不妨先追加样本量至23, 根据结果判断样本量是否充分, 重复（3）的过程; 如果 δ ′ _正 = 2.8次/分 < δ _专, 发现的差异只有2.8次/分, 有必要追加样本量, 由公式（1）知N_专= 37 < N′ _正 = 42, 故此时样本量应该追加至37, 并结束样本量的估计。

讨论二：若观察指标没有公认的专业意义上的容许误差, 通常建议用0.25倍或0.50倍的标准差来设定容许误差δ , 可以给定δ 的一个取值范围（0.25S, 0.50S）, t_{α , ∞} = t_{0.05, ∞} = 1.645, t_{β , ∞} = t_{0.01, ∞} =1.282, 代入公式（1）,

当δ = 0.50S时, N= N=[(tα+tβ)Sδ]2= N=[(1.645+1.282)S0.50S]2= 34.27 ≈ 35

当δ = 0.25S时, N= N=[(tα+tβ)Sδ]2= N=[(1.645+1.282)S0.25S]2= 137.08 ≈ 137

可见δ 取值的不同计算出的样本量差异很大, 如果开始就按照δ = 0.25S估算出的样本进行实验, 很有可能浪费人力和物力。此时, 不妨按照较小的样本量进行实验, 然后根据实验结果, 按照讨论一的步骤进行调整。

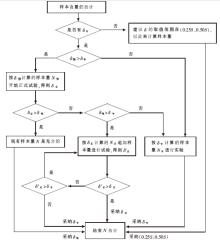
本文以单样本均数检验或均数的配对检验时的样本含量估计的情形为例, 根据有无专业意义上的公认的容许误差δ 分两种情况进行讨论, δ 取值不同, 计算的样本量不同, 有时甚至差异很大, 可以看出δ 的合理取值在样本量的估计中起到不可忽视的作用。为避免人力和物力的浪费, 有必要审慎对待假设检验时样本含量估计中δ 值的选取问题。对于其他需要使用容许误差完成样本量估算的情况, 同样适用前述推算步骤。在实际运用中可参考如下流程图（图1）。

图1

	Figure Option ViewDownloadNew Window
	图1 使用容许误差完成样本量估算的参考流程图

需说明的是, 有些抽样研究中增加观测对象数目并不会严重增加研究的成本, 这时, 对于样本量的估算就不必仿照这里的推算过程, 无需对估算的结果“ 斤斤计较” , 而应将估算出的样本量扩大至1.2、1.5乃至2倍用于实际样本量。这种情况下, 可以减少推算的反复次数。