引用本文
王佩鑫, 李宏田, 刘建蒙. 无对照二分类资料的Meta分析方法及Stata实现.循证医学, 2012, 12(1): 52-55
WANG Pei-xin, LI Hong-tian, LIU Jian-meng. Meta-Analysis of Non-Comparative Binary Outcomes and Its Solution by Stata. Journal of Evidence-based Medicine,2012, 12(1): 52-55  
Permissions
Copyright©2012, 《循证医学》杂志 版权所有
无对照二分类资料的Meta分析方法及Stata实现
王佩鑫a,b, 李宏田b,c, 刘建蒙b,c
北京大学 a. 公共卫生学院
b. 生育健康研究所
c. 卫生部生育健康重点实验室, 北京 100191
通讯作者:刘建蒙,Tel：010-85226877;E-mail：liujm@pku.edu.cn

作者简介:王佩鑫（1986-）,男,河北馆陶人,在读硕士研究生,研究方向为妇女儿童保健。

基金:国家自然科学基金资助项目（81072372）
摘要

目的 介绍无对照二分类资料Meta分析方法及在Stata软件中的操作步骤。方法 首先介绍3种数据类型无对照二分类资料Meta分析的原理及方法,再用Stata软件对3个实例数据进行Meta分析。结果 无对照二分类资料Meta分析的关键是选择服从正态分布或可转化为正态分布的指标。3个实例数据经正态转换后进行Meta分析,结果与原文一致。结论 Stata软件可实现无对照二分类资料（含患病率、发病密度和比值）的Meta分析,操作简单,实用性强。

关键词: 二分类变量; 无对照; Stata; Meta分析
中图分类号:R195.1 文献标识码:A 文章编号:1671-5144（2012）01-0052-04
Meta-Analysis of Non-Comparative Binary Outcomes and Its Solution by Stata
WANG Pei-xina,b, LI Hong-tianb,c, LIU Jian-mengb,c
a. School of Public Health
b. Institute of Reproductive and Child Health
c. Ministry of Health Key Laboratory of Reproductive Health, Peking University, Beijing 100191, China
Abstract

Objective To introduce the method of meta-analysis for non-comparative binary outcomes and its realization in Stata.Methods We first introduced principles and methods of meta-analysis for three types of non-comparative binary outcomes, and then replicated results of three published meta-analyses in Stata.Results The key point of doing these meta-analyses was to choose the effect size indices which were of normal distribution or could be transformed into normal distribution. The replicated results were consistent with the original literatures.Conclusions Meta-analyses for three types of binary outcomes, including prevalence, incidence density, and odds, could be done in Stata conveniently.

Key words : binary; non-comparative; Stata; meta-analysis

生物医学发展迅速, 科学工作者常需综合评价针对某一科学问题的不同研究证据。如何归纳和综合分析这些分散的研究证据, 提升对问题的认识水平, 已成为生物医学研究的重要步骤[1]。荟萃（Meta）分析就是定量综合分析多个同类研究效应的方法[2]。近十年, Meta分析在生物医学领域应用日益广泛, 有关文献迅速增多, 2001年前共有169篇中文论文发表, 而在2001-2009期间就有2 115篇。已发表的Meta分析多针对设有对照的研究类型, 国内文献未见针对无对照的研究类型如横断面研究, 国外亦少见。横断面研究等没有设对照的研究是人群研究的基础, 也是揭示暴露与疾病关系不可或缺的。生物医学工作者掌握针对无对照的研究类型的Meta分析方法和计算机实现步骤是必要的。本文旨在介绍二分类无对照资料的Meta分析方法及其在Stata软件中的操作步骤。

1 Meta分析方法介绍
1.1 各效应指标的异质性检验

进行Meta分析, 首先要对各研究的效应指标进行异质性检验。用i表示第i个研究的效应指标, 异质性检验的假设为：

H0： Q̂1= Q̂2 =…= Q̂k

H1： Q̂1, Q̂2, …, Q̂k不全相同

对效应指标进行异质性检验的统计量为：

Q = ∑i=1kWi(θ̂i-θ̂̅)2

Q服从自由度为k-1的χ 2分布。当拒绝H0时, 认为各个效应指标不全相等, 即各研究的效应指标异质。

1.2 模型的正确选择

根据异质性检验的结果, 选择并使用合适的模型进行指标合并。目前对模型的选择较为一致的看法是：当各研究的效应指标同质时, 选用固定效应模型或随机效应模型对结果影响不大。但各效应指标不同质时, 宜选用随机效应模型[3]。

固定效应模型的常用计算方法, 有倒方差法（inverse variance methods）、Mantel-Haenszel法（简称M-H法）、Peto法。倒方差法的应用范围较广, 但当二分类资料出现极端值时, 其稳定性不如M-H法; M-H法只适用于有四格表资料的二分类变量的研究结果[即危险率比（risk ratio, RR）、比值比（odds ratio, OR）、危险率差（risk difference, RD）]; Peto法又称为改进的M-H法。所以, M-H法与Peto法都要求资料有对照组数据。

随机效应模型主要有DerSimonian and Laird法（简称D-L法）。它的计算思路与倒方差法相同, 只是在各研究效应的基础上考虑了随机误差。

无对照、二分类变量的研究结果, 往往以患病率（prevalence）、发病密度（incidence density）或比值（odds）的形式表达。对于此类资料, 各研究间同质时, 其Meta分析应选择固定效应模型的倒方差法; 各研究间存在异质性时应选择随机效应模型的D-L法。

1.3 倒方差法的效应指标及其标准误

在倒方差法中, 各个研究的权重为 Wi=1(Sθθ̂2)2, 合并的效应指标的计算公式为 θ̂̅=∑Wiθ̂̅i∑Wi。而D-L法是在上面的计算方法上增加了随机误差变量。从上面的公式可以看到, 提取出合适（近似服从正态分布）的效应指标θ i, 以及计算出标准误se（ θ̂̅i）是关键。前述三类无对照、二分类变量研究资料的效应指标及其标准误的计算方法如下[4, 5]：

①如发病率（incidence）、患病率（prevalence）等分子与分母都为个数的结局指标：

θ̂i=Xn

seθ̂i=θi(1-θi)n-1≈θi(1-θi)n

其中, X为发生个数, n为总个数。为保证θ i能够近似满足正态分布, 此时n要求足够大, 且nθ i及n（1-θ i）均大于5。

②如发病密度（incidence density）等分母为人时的结局指标：

θ̂i=ln（inccidence density）=ln（d/q）

se（θ̂i）=se（lnincidence density)=1/d

其中, d为指定时间段内事件发生的个数, q为观察的人时。

③比值（odds）类的结局指标：

θ̂i=ln（Odds）=ln（mn）

se（θ̂i）=se（ln（Odds））=1m+1n

其中, m为某事件发生的个数, n为某事件未发生的个数。当患病率（prevalence）类数据不能满足正态分布时, 也可考虑使用这种方法。

2 实例分析

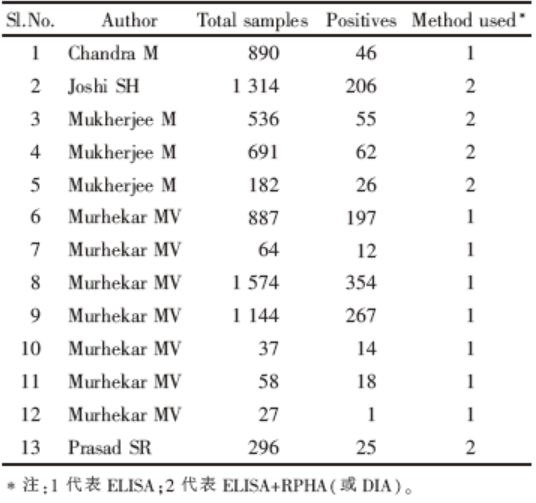
例1[6] 为研究乙型肝炎在印度的现患率, Batham等人检索了印度各地的乙肝现患率研究。其中, 有13个是对生活在部落地区的人群乙肝现患率的研究。数据如表1所示。

表1 13个部落地区人群的乙肝现患率研究数据

操作步骤：

第一步, 整理文献中提供的原始数据, 如表1所示。

第二步, 在Stata软件中录入数据, 初步产生分析变量。其中变量m表示Positives, 即阳性人数。n表示Total samples, 即调查的总人数。Methods表示诊断所使用的方法。录入结束后, 编写Stata命令, 产生初步的分析变量。命令如下：

gen p=m/n/∗产生Meta分析的指标变量

gen se=sqrt（p∗（1-p）/n）/∗产生指标变量的标准误

gen ll=p-1.96∗se/∗产生指标变量95%CI的下限

gen ul=p+1.96∗se/∗产生指标变量95%CI的上限

第三步, 对产生的初步分析变量进行校正。由于各诊断方法具有一定的灵敏度与特异度, 所以需要根据使用方法的不同对上面计算的率进行校正。校正公式为：

True prevalence=［Estimated prevalence－（1－specificity）］［Sensitivity－（1－specificity）］

对于方法1, 其灵敏度为99.8%, 特异度为99.8%; 对于方法2, 为两种方法连用, 其灵敏度与特异度都视为100.0%。所以根据上述公式, 对部分研究在第二步产生的p、ll、ul进行校正。校正命令如下：

replace p=（p-0.002）/0.996 if methods==1

replace ll=（ll-0.002）/0.996 if methods==1

replace ul=（ul-0.002）/0.996 if methods==1

第四步, 进行Meta分析。Stata命令如下：

metan p ll ul, random

计算结果的异质性检验：χ 2=361.64, df=12, P< 0.001, 存在异质性, 提示用随机效应模型。用D-L法合并的现患率为15.8%, 95%CI为11.3%~20.3%, 与原文一致。

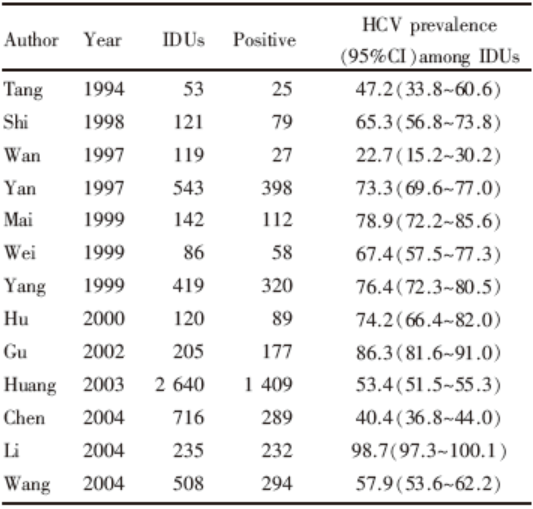
例2[7] 为调查中国静脉吸毒人群中丙肝的现患率, 南京医科大学喻荣彬等人收集了1994-2006年的大量相关研究。下面是广东省静脉吸毒人群丙肝现患率的各研究资料, 见表2所示。

表2 广东省静脉吸毒人群中丙肝的现患率研究数据

操作步骤：

第一步：整理文献中提供的原始数据, 如表2所示。

第二步：在Stata中录入数据。m表示乙肝阳性个体的数目, n表示总的调查人数, p表示HCV prevalence, ll表示prevalence 95%CI的下限, ul表示prevalence 95%CI的上限。

第三步：进行Meta分析。此时可尝试使用三种计算方式, 分别如下：

①方法一, 同例1所示, 直接利用p以及ll、ul进行计算, Stata命令如下：

metan p ll ul, random

计算结果的异质性检验：χ 2=2 238.27, df=12, P< 0.001, 存在异质性, 提示用随机效应模型。用D-L法合并的现患率为64.9%, 95%CI为50.9%~78.9%, 与原文一致。

②方法二, 利用效应指标θ i及其标准误se（ θ̂i）来进行Meta分析。因为此时的二项分布非常接近于正态分布, 所以可以按照符合正态分布的方法进行计算。Stata命令如下：

gen se=（ul-ll）/（1.96∗2）

meta p se, random

计算结果的异质性检验：χ 2=2 238.35, df=12, P< 0.001, 存在异质性, 提示用随机效应模型。用D-L法合并的现患率为64.9%, 95%CI为50.9%~78.9%, 与方法一完全一致。

③方法三, 利用比值（odds）类型数据的计算方法进行Meta分析。Stata命令如下：

gen t=n-m

gen pp=ln（m/t）

gen see=sqrt（1/m+1/t）

metan pp see, random eform

计算结果的异质性检验：χ 2=412.19, df=12, P< 0.001, 存在异质性, 提示用随机效应模型。用D-L法合并的odds=2.062, 95%CI为1.411~3.015。然后再做转换如下：

Prevalence = 2.0621+2.062= 67.3%

95%CI lower limit = 1.4111+1.411= 58.5%

95%CI upper limit = 3.0151+3.015= 75.1%

即利用这种方法最终合并的现患率为67.3%, 95%CI为58.5%~75.1%。现患率与前两种方法略有差别, 95%CI的范围与前两种方法相比“ 变窄” 了。这可能是由于这种方法与前两种方法在计算精度上存在不同所导致的。

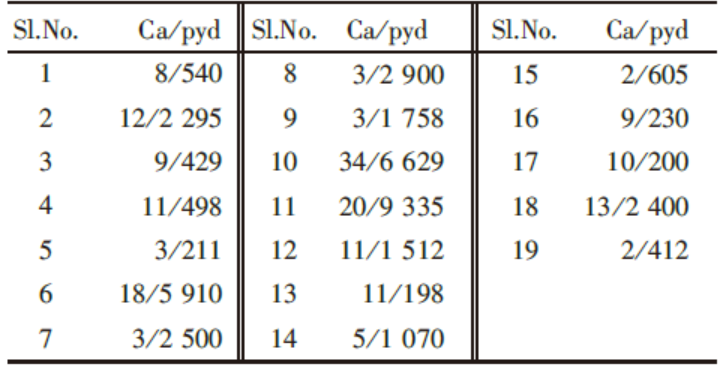
例3[8] 英国莱切斯特大学Eaden等对大肠溃疡患者发生结（直）肠癌的风险进行了Meta分析, 其纳入19篇以incidence rate作为结局指标的研究。数据摘录见表3所示。

表3 关于患大肠溃疡人群发生结（直）肠癌风险的研究数据

操作步骤：

第一步, 整理文献中提供的原始数据, 如表3所示。

第二步, 在Stata中输入数据。为了演示的方便, 该例只输入两个变量：d, 表示在研究的时间段内特定人群患结（直）肠的个数; q, 表示研究的时间段内, 特定研究人群的人年数。很显然, 该例数据为Incidence Density类型。所以编写Stata命令如下：

gen p=ln（d/q）

gen se=1/d

第三步, 进行Meta分析, 编写Stata命令如下：

metan p se, random eform

计算结果的异质性检验：χ 2=2 402.27, df=18, P< 0.001, 存在异质性, 提示用随机效应模型。用D-L法合并的incidence rate=0.007, 95%CI为0.005~0.011。即总的incidence rate为7/1 000 person years duration（pyd）, 95%CI为5/1 000~11/1 000 pyd, 和原文一致。

3 讨 论

Meta分析是定量综合既往研究资料的方法, 应用日益广泛。截止2010年底, PubMed收录的Meta分析文章达2.7万余篇。国内文献报告的Meta分析多针对有对照的研究资料, 未检索到针对无对照研究资料的Meta分析。应用较为广泛的Meta分析软件有Review Manager（RevMan）和Stata。相对RevMan来说, Stata操作灵活、简单易用, 可进行几乎所有类型的Meta分析, 如Meta回归、累积Meta分析、敏感性分析、发表偏倚的统计检验等[9]。为此, 本文介绍了无对照二分类资料的Meta分析方法及其在Stata中的实现。

通过倒方差法原理分析, 本文总结认为无对照二分类资料Meta分析的关键是选择服从正态分布、或可转化为正态分布的指标。这类资料的效应指标主要有患病率（prevalence）、发病密度（incidence density）、比值（odds）三种。对患病率类数据, 当样本量较大时即可满足正态分布, 样本量较小不满足正态分布时可转化为比值类数据进行分析。发病密度与比值类数据通过对数转换, 均可转化为正态分布的数据。但是, 比值类数据, 对“ 全发生” 或者“ 全不发生” 的情况束手无策, 即比值的分子分母不能为零。对这种情况下数据的Meta分析, 尚待研究。

The authors have declared that no competing interests exist.

参考文献
[1] 林杨, 李立明. 关于Meta-分析在医学领域的争鸣[J]. 中华流行病学杂志, 1999, 20(1): 53-54. [本文引用:2]
[2] 方积乾, 陆盈. 现代医学统计学[M]. 北京: 人民卫生出版社, 2002: 150-151. [本文引用:2]
[3] 凌莉, 韩璐. Meta分析方法的正确应用[J]. 循证医学, 2002, 2(2): 102-104. [本文引用:2]
[4] 方积乾. 卫生统计学[M]. 第6版, 北京: 人民卫生出版社, 2008. [本文引用:1]
[5] Sutton AJ, Abrams KR, Jones DR, et al. Methods for meta-analysis in medical research[M]. John Wiley & Sons, Ltd. 2000, Chichester, England . [本文引用:1]
[6] Batham A, Narula D, Toteja T, et al. Systematic review and meta-analysis of prevalence of hepatitis B in India[J]. Indian Pediatr, 2007, 44(9): 663-674. [本文引用:1] [JCR: 1.036]
[7] Xia X, Luo J, Bai J, et al. Epidemiology of hepatitis C virus infection among injection drug user in China: Systematic review and meta-analysis[J]. Public Health, 2008, 122(10): 990-1003. [本文引用:1] [JCR: 1.35]
[8] Eaden JA, Abrams KR, Mayberry JF. The risk of colorectal cancer in ulcerative colitis: A meta-analysis[J]. Gut, 2001, 48(4): 526-535. [本文引用:1] [JCR: 10.732]
[9] 柏建岭, 钟文昭, 郑明华, 等. Stata 在Meta 分析中的应用[J]. 循证医学, 2007, 7(6): 363-368. [本文引用:1]