作者简介: 张天嵩(1970#cod#x02013;),男,山东昌邑人,医学博士,主任医师, 副教授,从事呼吸系统疾病中西医结合临床及循证医学方法学研究。
目的 介绍有序数据的Meta分析方法及其在SAS软件的实现。方法 以实例说明,采用两步法:第一步,基于累积比数模型,采用SAS中的GENMOD过程计算产生每个研究的效应量及其标准误;第二步,采用固定效应模型和随机效应模型以SAS中的MIXED过程进行经典Meta分析。结果 固定效应和随机效应模型Meta分析结果显示,汇总比值比及95%可信区间均为2.853 9 (2.106 4,3.864 8)。结论 对于有序数据,可以应用SAS中的GENMOD过程和MIXED过程进行Meta分析。
Objective To introduce methodology for undertaking a meta-analysis on ordinal data and its realization in SAS.Methods It was illustrated on an example data by using two-step method. In the first step, it was calculated treatment effect and its standard error for an individual study by using PROC GENMOD in SAS based on cumulative odds models; in the second step, a classical meta-analysis was proposed for fixed and random effect model by using PROC MIXED in SAS.ResultsResults from the traditional meta-analysis of summary odds ratio and its 95%CI were same 2.853 9(2.106 4,3.864 8) for fixed and random effect model.Conclusions The procedure SAS PROC GENMOD and MIXED were utilized to undertake a meta-analysis on ordinal data.
在过去的25年中, Meta分析作为一种汇总多个研究结果而进行总体效应评价的科学研究方法, 已广泛应用于社会和医学科学研究中[1], 它是采用科学合理的统计学方法汇总多个具有相同研究目的的同类研究结果, 对于二分类数据和连续型数据, 目前已有比较完善的统计分析方法。但在实践中很多临床结局采用有序分类尺度进行测量[2], 其结果常常为多分类且有序的等级资料, 例如治疗效果的“ 治愈、显效、有效、无效” 等。对于此类有序或序次数据, 采用经典的Meta分析方法较难处理[2]。而根据具有相当影响力的Cochrane手册处理方法, 一是选取适当的切割点, 将数据合并为二分类数据; 二是通过计分转化为连续型数据[3], 但可能难以利用全部资料的信息, 因此, 对此类数据的Meta分析需要进一步研究, 本文在复习文献基础上, 提供一种基于累积比数模型的分析方法及其在SAS软件中的实现。
假设临床结果变量为有m个等级的有序分类变量C1, C2, …, Cm等, 将C1定义为最佳, Cm为最差, 数据可整理成2× m行列表格式, 如表1。
| 表1 2× m行列表有序数据格式 |
假设结果变量为m个等级的有序分类变量, k为有序变量的某一等级, 此时可将m个等级分为两类:等级小于等于k的(C1, …Ck)为一类, 定义为治疗成功; 等级大于k(Ck+1, …Cm)的为一类, 定义治疗失败。假设治疗组和对照组患者第k类的机率为pkT、pkC, 则等级小于等于k的累积概率分别为[4]:
QkT = p1T +…+pkT, QkC = p1C +…+pkC, k =1, …, m
治疗组治疗成功与失败的概率分别为QkT与1-QkT; 对照组治疗成功与失败的概率分别为QkC与1-QkC。
令研究间的效应量为:
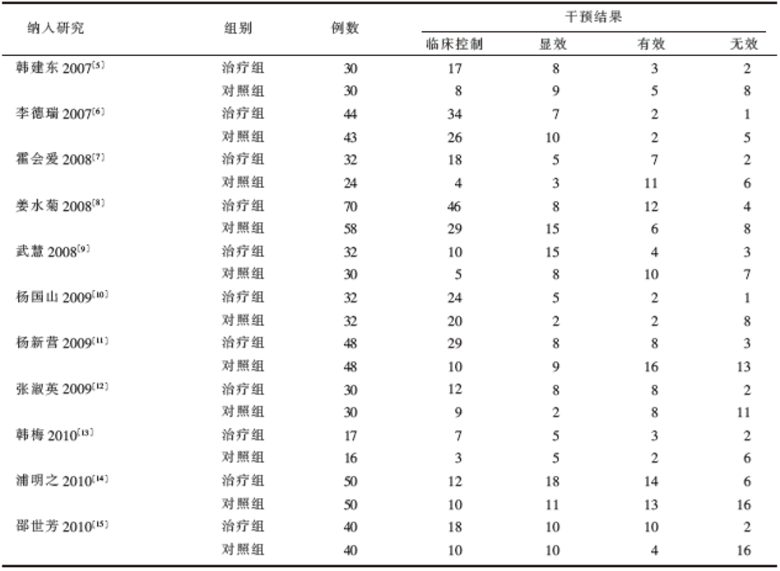
以我们的研究课题数据为例, 观察中西医结合治疗咳嗽变异性哮喘的疗效, 治疗组干预措施为宣肺止咳中药加用西药, 对照组为单纯西药, 共收集到11个符合标准的研究, 按表1格式整理, 具体数据如表2。
| 表2 中西医结合治疗咳嗽变异性哮喘随机对照试验干预结果 |
我们以SAS的GENMOD过程来计算每个研究的效应量, 如对于第一个研究, SAS程序如下:
data study1;
input treatment effect cases;
datalines;
1 1 17
1 2 8
1 3 3
1 4 2
0 1 8
0 2 9
0 3 5
0 4 8
proc print;
run;
proc GENMOD data = study1;
weight cases;
model effect = treatment/dist = multinomial link = cumlogit; /∗拟合有序多分类
logistic回归模型(累积logistic)模型∗/
run;
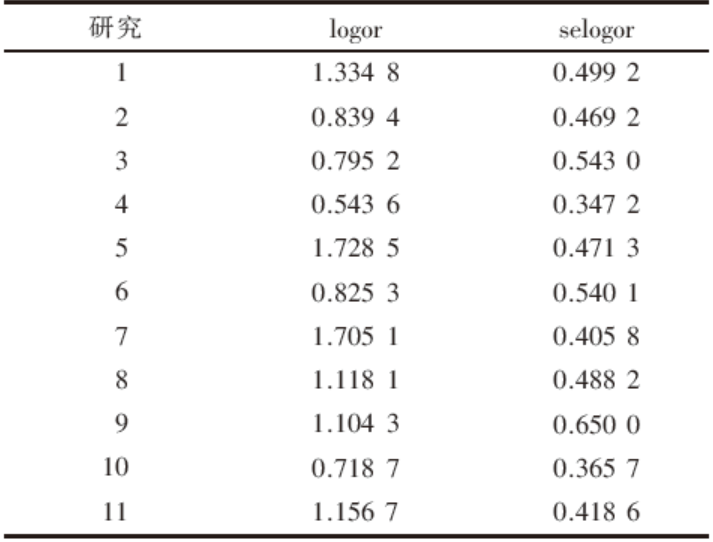
可以得到第一个研究的效应量(logor)及其标准误(selogor)为1.334 8和0.499 2, OR=e1.334 8=3.799, 其含义为, 与对照组相比, 治疗组疗效提高一个及一个以上的等级(如由“ 有效” 提高到“ 临床控制” )的可能性增加了279.9%。同样可以得到其他研究的效应量及其标准误, 如表3。
| 表3 各研究的效应量及其标准误 |
方法与经典的Meta分析相同, 可以合并11个研究的效应量, 众多软件可以完成。我们以SAS的MIXED过程来实现[16], 其结果见表4。
| 表4 合并效应量结果 |
固定效应模型SAS程序如下:
data mstudy;
input study logor selogor;
datalines;
1 1.3348 0.4992
2 0.8394 0.4692
3 0.7952 0.5430
4 0.5436 0.3472
5 1.7285 0.4713
6 0.8253 0.5401
7 1.7051 0.4058
8 1.1181 0.4882
9 1.1043 0.6500
10 0.7187 0.3657
11 1.1567 0.4186
run;
data newmstudy;
set mstudy;
est = selogor∗∗2; /∗计算每个研究的方差∗/
keep study logor est;
run;
proc mixed method = ml data = newmstudy;
class study;
model logor = / s cl; /∗截距模型; 要求打印
固定效应估计值, 并显示95%CI∗/
repeated /group = study;
parms / parmsdata = newmstudy
eqcons = 1 to 11;
run;
随机效应模型SAS程序如下:
data covvars;
set newmstudy;
keep est;
run;
data start;
input est;
cards;
0.0
run;
data start;
set start covvars;
run;
proc mixed method = ml cl data = newmstudy;
class study;
model logor = / s cl;
random int / subject = study; /∗指定研究为
随机效应∗/ repeated / group = study;
parms / parmsdata = start
eqcons = 2 to 12;
run;
累积比数模型又称为比例优势模型(proportional odds model)、累积比数logit模型、有序logit模型(ordinal logit model), 是二分类logit模型的扩展, 主要用于处理反应变量为有序分类变量的资料。该模型对资料要求相对不严, 解释变量可以是连续型数据, 也可以是无序分类变量或有序分类变量[17], 只要资料满足比例优势假定条件, 即自变量的回归系数与分割点无关[18], 然而在实际应用中可不必拘泥于此, 因为该模型对上述条件并不敏感, 即当该条件不成立时, 参数估计仍然较稳定, 故此法适用范围较为广泛[19]。
本文基于累积比数模型, 以实例说明采用两步法对有序数据进行Meta分析的步骤:第一步, 以累积比数模型, 采用SAS中的GENMOD过程来计算产生每个研究的效应量及其标准误; 第二步为经典的Meta分析方法, 可以使用合适的模型对第一步产生的数据进行Meta分析, 相对比较简单。为节省篇幅, 本文没有进行异质性检验、发表偏倚检验, 仅分别演示了应用SAS软件MIXED过程来进行固定效应模型和随机效应模型Meta分析。有兴趣的读者可以阅读相关文献, 采用SAS软件做异质性检验、发表偏倚检验等, 也可选用RevMan、Stata等其他软件来实现。
对于有序分类反应变量资料的Meta分析, 既应该考虑其结果的多分类形式, 又要考虑到结果的有序性, 本文提供的基于累积比数模型是处理此类资料的一种方法, 至于其他方法将另行撰文介绍。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|