网络Meta分析在R软件中的实现

引用本文

张天嵩, 熊茜. 网络Meta分析在R软件中的实现.循证医学, 2012, 12(3): 185-188
ZHANG Tian-song, XIONG Qian. Network Meta-Analysis and Its Solution by R. Journal of Evidence-based Medicine, 2012,12(3): 185-188 复制到剪切板

Permissions

网络Meta分析在R软件中的实现

张天嵩^a,^b, 熊茜^a

上海市静安区中心医院 a. 科教部

b. 中医科, 上海 200040

作者简介：张天嵩（1970#cod#x02013;）,男,山东昌邑人,医学博士,主任医师,副教授,主要从事呼吸系统疾病的中西医结合治疗及循证医学方法学研究。

摘要

目的介绍网络Meta分析方法及其在R软件的实现。方法以实例说明,采用R软件lme（）函数,通过对来自5个预防人类免疫缺陷病毒感染者发生复合鸟分支杆菌感染事件随机对照研究的3种药物和安慰剂进行直接和间接比较,进行网络Meta分析。结果直接和间接比较结果表明,所有药物较之于安慰剂均可以减少人类免疫缺陷病毒感染者出现复合鸟分支杆菌事件发生,克拉霉素和阿奇霉素较之于利福平均可以减少人类免疫缺陷病毒感染者出现复合鸟分支杆菌事件发生;而对无直接比较证据的克拉霉素与阿奇霉素,间接比较结果显示两者差异无统计学意义。结论合并多个干预措施效果和没有所有干预措施直接比较证据时,采用网络Meta分析方法合并直接和间接比较结果是一种正规的方法。

关键词: 网络Meta分析; 线性混合效应模型; 间接比较; R软件

中图分类号:R195.1 文献标识码:A 文章编号:1671-5144（2012）03-0185-04

Network Meta-Analysis and Its Solution by R

ZHANG Tian-song^a,^b, XIONG Qian^a

a. Department of Science & Education

b. Department of TCM, Jing’an District Central Hospital, Shanghai 200040, China

Abstract

Objective To introduce methodology for undertaking a network meta-analysis and its realization in R. Methods By using lme（） function in R, network meta-analysis of randomized controlled trials（RCTs） was used to combine direct and indirect estimates of the effect of three drugs and placebo for mycobacterium avium complex （MAC） in patients infected with the human immunodeficiency virus （HIV） from 5 RCTs. Results All drugs differed from placebo in reducing MAC events from the results of direct and indirect comparisons. Clarithromycin and Azithromycin differed from Rifabutin in reducing MAC events from the results of direct and indirect comparisons respectively. The indirect efficacy of Clarithromycin and Azithromycin had no significance in statistically. Conclusions A network meta-analysis can be used to combine direct and indirect treatment effects in a formal when several treatments are available and not all treatments have been compared directly in some two-armed RCTs.

Key words : network meta-analysis; linear mixed-effects model; indirect comparisons; R

Show Figures

在理想情况下, 直接比较某一干预措施与对照或阳性药物的随机对照试验是评价治疗效应的金标准, 但在实际情况下, 许多干预措施缺乏或没有直接比较的证据^[1]。随着医学研究的进展, 在没有直接证据时, 越来越需要干预措施间接比较的证据。采用网络Meta分析可以同时进行直接与间接比较, 即使是相比较的两种治疗药物从未进行过直接对比, 这种分析方法可以将一系列不同治疗方法随机临床试验数据汇总, 然后就给定的治疗终点进行点估计及可信区间估计, 同时对非相关性进行评估, Lumley教授首先提出了网络Meta分析（network meta-analysis）的模型和方法^[2], 可以在多种统计软件中通过拟合线性混合效应模型而实现, 本文以实例说明以R14.1的“ nlme” 软件包来进行网络Meta分析的具体过程。

1 数据来源

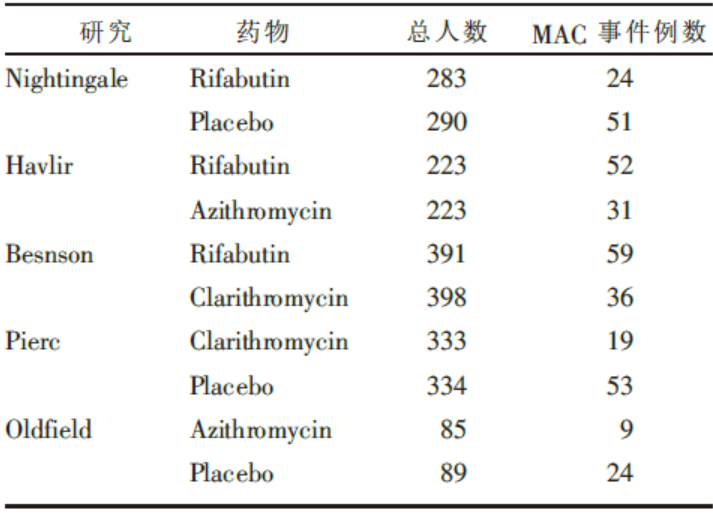
该方法需要数量较多的干预措施比较研究, 但限于篇幅和简便说明起见, 我们采用一简单数据为例, 其源于公开发表的文献^[3], 含有五个研究, 主要观察药物预防人类免疫缺陷病毒感染者出现复合鸟分支杆菌（mycobacterium avium complex, MAC）事件例数, 其用药物、患者数、出现MAC事件人数具体见表1。

表1 实例数据

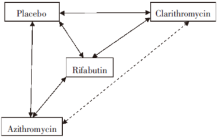
从表1中可以看出, 有“ Rifabutin与Placebo” 、“ Clarithromycin 与Placebo” 、“ Azithromycin 与Placebo” 、“ Rifabutin 与Clarithromycin” 直接比较的证据, 图1中以实线表示, 但无“ Clarithromycin与Azithromycin” 直接比较的证据, 但可以通过网络Meta分析来计算出间接比较的证据。

	Figure Option View Download New Window
	图1 药物直接比较与间接比较网络图

2 数据预处理

为了进行网络Meta分析, 必须对表中的数据进行预处理, 使之适宜于线性混合模型分析的要求。将数据整理成两两比较形式, 共得到5个比较组, 按经典方法, 分别计算出两比较组的对数比数比（logor）及其标准误（selogor）; 将配对比较的药物分别记为1与-1, 无关的药物记为0, 预处理后的数据见表2。

表2 预处理后的数据

3 网络Meta分析的具体步骤

以“ nlme” 扩展包中lme（）函数来实现网络Meta分析, 具体过程如下：

第一步：读入数据, 将表中的数据输入Excel表格中, 输入完成后, 将其另存为“ 文本文件（制表符分隔）（∗.txt）” , 并命名为“ hiv-ma.txt” , 假设存储在C盘根目录下。在R软件命令输入窗口分别键入：

> library（foreign）

> mydata< -read.table（"c：/hiv-ma.txt", header=TRUE）

> mydata < - transform（mydata, trtpair = paste（drug1, drug2））

上述命令是将数据读入, 建立一个名为“ mydata” 的数据集, 并经过处理, 将两两比较的药物结成对子, 以便于进一步分析。

第二步：进行网络Meta分析, 在R软件命令输入窗口分别键入：

> library（nlme）

> lme1 < - lme（logor ~ 0 + Rifabutin + Clarithromycin + Placebo, random = ~ 1 | trtpair, data=mydata, weights = varConstPower（form=~selogor, fixed=list（power=1）））

上述命令是载入“ nlme” 扩展包, 采用lme（）函数拟合线性混合效应模型。其中“ logor ~0 + Rifabutin + Clarithromycin + Placebo” 为固定效应; “ random = ~ 1 | trtpair” 表示以药物配对为随机效应。

键入summary（lme1）查看结果, 主要结果有：

Linear mixed-effects model fit by REML

Data： mydata

AIC BIC logLik

12．2479 4．406784 – 0．1239505

Random effects：

Formula： ~1 | trtpair

（Intercept） Residual

StdDev： 0．1530756 7．519467e-05

Variance function：

Structure： Constant plus power of variance covariate

Formula： ~selogor

Parameter estimates：

const power

0．07291978 1．00000000

Fixed effects： logor~0 + Rifabutin + Clarithromycin + Placebo

Value Std．Error DF t-value p-value

Rifabutin 0．5440413 0．1210168 2 4．495583 0．0461

Clarithromycin 0．0264223 0．1530756 2 0．172610 0．8788

Placebo 1．2262220 0．1210168 2 10．132655 0．0096

Correlation：

Rifbtn Clrthr

Clarithromycin 0．632

Placebo 0．600 0．632

Standardized Within-Group Residuals：

Rifabutin Placebo Rifabutin Azithromycin

– 1．639448e-04 9．230187e-05

Rifabutin Clarithromycin Clarithromycin Placebo

6．008755e-05 7．118959e-05

Azithromycin Placebo

1．425168e-04

Number of Observations： 5

Number of Groups： 5

在结果的随机效应估计部分, 其截距标准差代表网络不相关性, 其数值越小表明网络越稳定; 固定效应估计部分, 以“ Azithromycin” 为参照药物, 其他三种药物分别与其相对比较的logor及其标准误、相应P值, 从而可以求得其间接比较的比数比（odds ratio, OR）及其95%可信区间（confidence interval, CI）, 如得到“ Clarithromycin vs. Azithromycin” 间接比较的OR及95%CI为1.03（0.76, 1.39）。

两种药物预防MAC事件出现直接和间接比较结果（OR及95%CI）见表3, 表中右上部分是直接比较的结果（横向排列药物为参照）, “ Clarithromycin” 与“ Azithromycin” 没有直接比较的结果; 左下部分以浅灰色为底标记的数据是间接比较的结果（纵向排列药物为参照）。直接比较和间接比较均提示三种药物均较之于“ Placebo” 、“ Azithromycin” 和“ Clarithromycin” 较之于“ Rifabutin” 可降低发生MAC事件的风险, 而且直接比较和间接比较结果是一致的; 而“ Azithromycin” 和“ Clarithromycin” 在降低MAC发生风险方面无明显差异; 同时还发现间接比较的结果更为精确些。

表3 直接比较与间接比较获得结果比较

4 讨论

在没有直接比较的证据或者在比较两个以上干预措施有效性时, 必然会涉及间接比较^[4], 间接比较结果在理论上可能比直接比较结果准确, 但其证据级别低于直接比较的证据^[4], 如比较A和B两种干预措施的有效性, 尽管没有A干预措施和B干预措施直接比较的随机对照研究, 但有A干预措施与安慰剂比较和B干预措施与安慰剂比较的随机对照研究, 由此可能会获得A干预措施和B干预措施效应量的间接比较结果, 但其证据级别低于直接比较A干预措施和B干预措施的证据级别, 因此当两种证据都存在时, 首先考虑使用直接比较的证据^[5]。虽然间接比较的证据力度存在争议, 但众多学者不断探讨间接比较Meta分析方法学, 目前常用的有“ 网络 Meta分析（network meta-analyses, NMA）” 、“ 混合治疗比较（mixed treatment comparison, MTC）” 、“ 多种干预措施Meta分析（multiple treatments meta-analysis, MTC）” 等^[5], 这些Meta分析方法可以通过概率统计或贝叶斯方法来实现^{[2, 6]}。

网络 Meta分析是由Lumley建立的一种用于间接比较的方法, 可以获得直接和间接比较的结果。该方法基于线性混合效应模型, 包括两个随机效应模型：研究水平的异质性、直接比较与间接比较结果比较的非一致性（即不相关性）, 只有当网络中的比较对象形成一个闭合环（如图1）时, 才能估算不相关性^[2], 但未提供不相关性大小的切割点。R软件属于GNU系统的一个自由、免费、开源软件, 是一套完整的数据处理、计算和绘图软件系统, 大多数经典的统计方法和最新的技术都可以在 R 中直接得到, R14.1自带“ nlme” 包, 目前最新版本为3.1-103, 可以拟合线性和非线性混合模型, 其中lme（）函数的基本功能为拟合线性混合效应模型, 可以实现Lumley氏法间接比较, 具体参数用法详见“ nlme” 包的说明文件^[7], 在此不赘述。

值得注意的是, 如果间接比较的研究中含有三个及以上的干预组时, Lumley氏网络Meta分析方法不适用, 应该考虑使用基于贝叶斯方法的MTC, 笔者将另行撰文详述。但不管采用何种方法, 进行间接比较时, 针对收集到的临床研究及数据, 需要评价其同质性、相似性和一致性, 这对于确保结果的有效性和可靠性非常重要^[8]。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Thijs V, Lemmens R, Fieuws S. Network meta-analysis: Simultaneous meta-analysis of common antiplatelet regimens after transient ischaemic attack or stroke[J]. Eur Heart J, 2008, 29(9): 1086-1092. [本文引用:1] [JCR: 14.097]
[2]	Lumley T. Network meta-analysis for indirect treatment comparisons[J]. Stat Med, 2002, 21(16): 2313-2324. [本文引用:3] [JCR: 2.044]
[3]	Chu J, Sloan CE, Freedberg KA, et al. Drug efficacy by direct and adjusted indirect comparison to placebo: An illustration by Mycobacterium avium complex prophylaxis in HIV[J]. AIDS Res Ther, 2011, 8: 14. [本文引用:1]
[4]	Guyatt GH, Oxman AD, Kunz R, et al. GRADE guidelines: 8. Rating the quality of evidence-indirectness[J]. J Clin Epidemiol, 2011, 64(12): 1303-1310. [本文引用:2] [JCR: 5.332]
[5]	Higgins JPT, Green S(eds). Cochrane Hand book for Systematic Reviews of Interventions Version 5. 1. 0[updated March 2011]. http: //www. cochrane-hand book. org [本文引用:2]
[6]	Lu G, Ades AE. Combination of direct and indirect evidence in mixed treatment comparisons[J]. Stat Med, 2004, 23(20): 3105-3124. [本文引用:1] [JCR: 2.044]
[7]	Pinheiro J, Bates D, DebRoy S, et al. Package ′nlme′www. cran. r-project. org/web/packages/nlme/nlme. pdf [本文引用:1]
[8]	Song F, Loke YK, Walsh T, et al. Methodological problems in the use of indirect comparisons for evaluating healthcare interventions: Survey of published systematic reviews[J]. BMJ, 2009, 338: b1147. [本文引用:1]

2008

14.097

0.0

... 在理想情况下,直接比较某一干预措施与对照或阳性药物的随机对照试验是评价治疗效应的金标准,但在实际情况下,许多干预措施缺乏或没有直接比较的证据^[1] ...

2002

2.044

0.0

Lumley

Network meta-analysis for indirect treatment comparisons[J]. Stat Med, 2002, 21(16): 2313-2324.

Department of Biostatistics, University of Washington, Box 357232, Seattle, WA 98195-7232, U.S.A. * Department of Biostatistics, University of Washington, Box 357232, Seattle, WA 98195-7232, U.S.A.

> I present methods for assessing the relative effectiveness of two treatments when they have not been compared directly in a randomized trial but have each been compared to other treatments. These network meta-analysis techniques allow estimation of both heterogeneity in the effect of any given treatment and inconsistency (‘incoherence’) in the evidence from different pairs of treatments. A simple estimation procedure using linear mixed models is given and used in a meta-analysis of treatments for acute myocardial infarction. Copyright © 2002 John Wiley & Sons, Ltd.

... 采用网络Meta分析可以同时进行直接与间接比较,即使是相比较的两种治疗药物从未进行过直接对比,这种分析方法可以将一系列不同治疗方法随机临床试验数据汇总,然后就给定的治疗终点进行点估计及可信区间估计,同时对非相关性进行评估,Lumley教授首先提出了网络Meta分析（network meta-analysis）的模型和方法^[2],可以在多种统计软件中通过拟合线性混合效应模型而实现,本文以实例说明以R14 ...

... 等^[5],这些Meta分析方法可以通过概率统计或贝叶斯方法来实现^[2,6] ...

... 该方法基于线性混合效应模型,包括两个随机效应模型：研究水平的异质性、直接比较与间接比较结果比较的非一致性（即不相关性）,只有当网络中的比较对象形成一个闭合环（如图1）时,才能估算不相关性^[2],但未提供不相关性大小的切割点 ...

2011

0.0

... 1 数据来源该方法需要数量较多的干预措施比较研究,但限于篇幅和简便说明起见,我们采用一简单数据为例,其源于公开发表的文献^[3],含有五个研究,主要观察药物预防人类免疫缺陷病毒感染者出现复合鸟分支杆菌（mycobacterium avium complex,MAC）事件例数,其用药物、患者数、出现MAC事件人数具体见表1 ...

2011

5.332

0.0

Guyatt

, Oxman

, Kunz

, et al. GRADE guidelines: 8. Rating the quality of evidence-indirectness[J]. J Clin Epidemiol, 2011, 64(12): 1303-1310.

Abstract Direct evidence comes from research that directly compares the interventions in which we are interested when applied to the populations in which we are interested and measures outcomes important to patients. Evidence can be indirect in one of four ways. First, patients may differ from those of interest (the term applicability is often used for this form of indirectness). Secondly, the intervention tested may differ from the intervention of interest. Decisions regarding indirectness of patients and interventions depend on an understanding of whether biological or social factors are sufficiently different that one might expect substantial differences in the magnitude of effect. Thirdly, outcomes may differ from those of primary interest—for instance, surrogate outcomes that are not themselves important, but measured in the presumption that changes in the surrogate reflect changes in an outcome important to patients. A fourth type of indirectness, conceptually different from the first three, occurs when clinicians must choose between interventions that have not been tested in head-to-head comparisons. Making comparisons between treatments under these circumstances requires specific statistical methods and will be rated down in quality one or two levels depending on the extent of differences between the patient populations, co-interventions, measurements of the outcome, and the methods of the trials of the candidate interventions.

... 4 讨论在没有直接比较的证据或者在比较两个以上干预措施有效性时,必然会涉及间接比较^[4],间接比较结果在理论上可能比直接比较结果准确,但其证据级别低于直接比较的证据^[4],如比较A和B两种干预措施的有效性,尽管没有A干预措施和B干预措施直接比较的随机对照研究,但有A干预措施与安慰剂比较和B干预措施与安慰剂比较的随机对照研究,由此可能会获得A干预措施和B干预措施效应量的间接比较结果,但其证据级别低于直接比较A干预措施和B干预措施的证据级别,因此当两种证据都存在时,首先考虑使用直接比较的证据^[5] ...

0.0

... 等^[5],这些Meta分析方法可以通过概率统计或贝叶斯方法来实现^[2,6] ...

2004

2.044

0.0

, Ades

AE.

Combination of direct and indirect evidence in mixed treatment comparisons[J]. Stat Med, 2004, 23(20): 3105-3124.

MRC HSRC, Department of Social Medicine, University of Bristol, U.K. * Canynge Hall, White Ladies Road, Bristol BS8 2PR, U.K.

> Mixed treatment comparison (MTC) meta-analysis is a generalization of standard pairwise meta-analysis for A vs B trials, to data structures that include, for example, A vs B, B vs C, and A vs C trials. There are two roles for MTC: one is to strengthen inference concerning the relative efficacy of two treatments, by including both ‘direct’ and ‘indirect’ comparisons. The other is to facilitate simultaneous inference regarding all treatments, in order for example to select the best treatment. In this paper, we present a range of Bayesian hierarchical models using the Markov chain Monte Carlo software WinBUGS. These are multivariate random effects models that allow for variation in true treatment effects across trials. We consider models where the between-trials variance is homogeneous across treatment comparisons as well as heterogeneous variance models. We also compare models with fixed (unconstrained) baseline study effects with models with random baselines drawn from a common distribution. These models are applied to an illustrative data set and posterior parameter distributions are compared. We discuss model critique and model selection, illustrating the role of Bayesian deviance analysis, and node-based model criticism. The assumptions underlying the MTC models and their parameterization are also discussed. Copyright © 2004 John Wiley & Sons, Ltd.

... 等^[5],这些Meta分析方法可以通过概率统计或贝叶斯方法来实现^[2,6] ...

0.0

... 包的说明文件^[7],在此不赘述 ...

2009

0.0

... 但不管采用何种方法,进行间接比较时,针对收集到的临床研究及数据,需要评价其同质性、相似性和一致性,这对于确保结果的有效性和可靠性非常重要^[8] ...