引用本文
张天嵩, 熊茜. HSROC模型在诊断试验Meta分析中的应用及Stata实现.循证医学, 2012, 12(4): 241-243
ZHANG Tian-song, XIONG Qian. HSROC Model in Meta-Analysis of Diagnostic Test and Its Solution in Stata. Journal of Evidence-based Medicine, 2012,12(4): 241-243  
Permissions
Copyright©2012, 《循证医学》杂志 版权所有
HSROC模型在诊断试验Meta分析中的应用及Stata实现
张天嵩a,b, 熊茜a
上海市静安区中心医院 a. 科教部
b. 中医科, 上海 200040

作者简介:张天嵩（1970-）,男,山东昌邑人,医学博士,主任医师,副教授,主要从事呼吸系统疾病的中西医结合治疗及循证医学方法学研究。

摘要

目的介绍HSROC模型在诊断试验Meta分析中的应用。方法 通过对实例中的数据采用Stata中“metandi”命令来拟合HSROC模型,进行Meta分析。结果 通过拟合模型,可以获得双变量模型、HSROC模型、经典统计指标等多个汇总合并结果。结论 HSROC模型用于诊断试验评价是恰当的、灵活的, 可作为经典 SROC法的改进和补充。

关键词: Meta分析; 诊断试验; 层次综合受试者工作特征模型
中图分类号:R195.1 文献标识码:A 文章编号:1671-5144（2012）04-0241-03
HSROC Model in Meta-Analysis of Diagnostic Test and Its Solution in Stata
ZHANG Tian-songa,b, XIONG Qiana
a. Department of Science & Education
b. Department of Traditional Chinese Medicine, Jing’an District Central Hospital, Shanghai 200040, China
Abstract

Objective To introduce the application of hierarchical summary receiver operating characteristic（HSROC） model in meta-analysis of diagnostic test.Methods We conducted meta-analysis to fit HSROC model by using the metandi command in Stata through the data of examples.Results The bivariate, HSROC parameter estimates and the summary point of estimates for traditional meta-analysis were obtained.Conclusions The HSROC model is appropriate and agile for diagnostic test, and could be used as an extension and improvement of the traditional SROC.

Key words : meta-analysis; diagnostic test; hierarchical summary receiver operating characteristic model

试验结果的Meta分析较经典的随机对照试验的Meta分析更加复杂, 目前理论上广泛接受的是构造综合受试者工作特征（receiver operating characteristic, ROC）曲线, 该法全面考虑了不同诊断界值下的诊断试验效果[1], 将各研究的灵敏度和特异度转换成单一的诊断准确度指标, 即诊断试验优势比, 其不足之处是缺乏鉴别灵敏度与特异度的能力, 忽略了由于诊断阈值不同产生的效应差异[2]。鉴于此, 近年来国内外学者提出几种关于诊断试验Meta分析的新策略, 如层次综合受试者工作特征曲线（hierarchical summary receive operating characteristic, HSROC）模型、双变量混合效应（bivariate mixed effects）模型等, 值得推广和应用, 后者国内已有学者具体介绍[1, 2], 本文以实例说明, 着重介绍HSROC模型及其在Stata软件中的实现。

1 资料与方法
1.1 资料来源

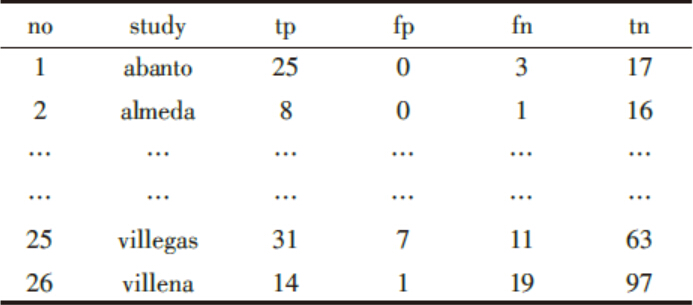
以文献中数据为例[3], 部分数据如表1所示, 共有26个研究, 每个研究根据Pai等[4]介绍的方法计算出真阳性数（true positive, tp）、假阳性数（false positive, fp）、假阴性数（false negative, fn）及真阴性数（true negative, tn）, 以“ no” 、“ study” 分别表示研究序号和名称。

表1 26 个结核性胸膜炎in-house NAA test 研究数据
1.2 HSROC模型

HSROC模型由Rutter等[5]提出, 是对固定效应综合受试者工作特征曲线模型的扩展, 用于合并评价多个诊断研究的灵敏度和特异度这一常用配对指标[5], 假设研究i中某一患者疾病状态j的阳性概率为π ij, 其中j=0表示无病, j=1表示有病, 因此灵敏度PAi=π il, 特异度PBi=1-π i0, 则HSROC模型为：

水平1（研究内）：log it（π ij）=（θ i+α iXij）exp（-β Xij）

水平2（研究间）：θ i~N（Θ , σ 2θ ）; α i~N（Λ , σ 2α ）

其中Xij=-0.5表示无病, Xij=0.5表示有病; θ i为切割点参数, 表示阳性域值, 其均数和方差分别为Θ 、σ 2θ ; α i为精确度参数, 其均数和方差分别设为Λ 、σ 2α ; β 为尺度参数, 表示ROC曲线不对称性。因此, 该模型中实际含有Λ 、Θ 、β 、σ 2α 、σ 2θ 五个参数。

1.3 HSROC模型在Stata中的实现方法

在上述模型中如果没有协变量, 可用Harbord等[6]为Stata编写的“ metandi” 命令来拟合, 其命令行操作格式为：

metandi tp fp fn tn, [参数]

其中, 常用的参数为：

plot：绘制SROC图; force：如果纳入研究中的一个或多个研究, tp+fn=0或tn+fp=0时, 强制“ metandi” 拟合数据; ip（g|m）：指定求积方法, 默认ip（g）为笛卡尔积, 以“ gllamm” 命令拟合模型（需要指定“ gllamm” 参数）时选用ip（m）; nip（#）：指定积分点, 默认为5, 数值越大精确度越高; nobivariate、nohsroc、nosummarypt：分别为不显示双变量模型、不显示HSROC模型、不显示经典诊断试验指标合并量等结果。

对于资料中的数据, 如果采用默认参数拟合HSROC模型, 并绘制层次综合ROC图, 在Stata软件命令行中键入命令：

metandi tp fp fn tn, plot

2 结 果
2.1 数字化结果

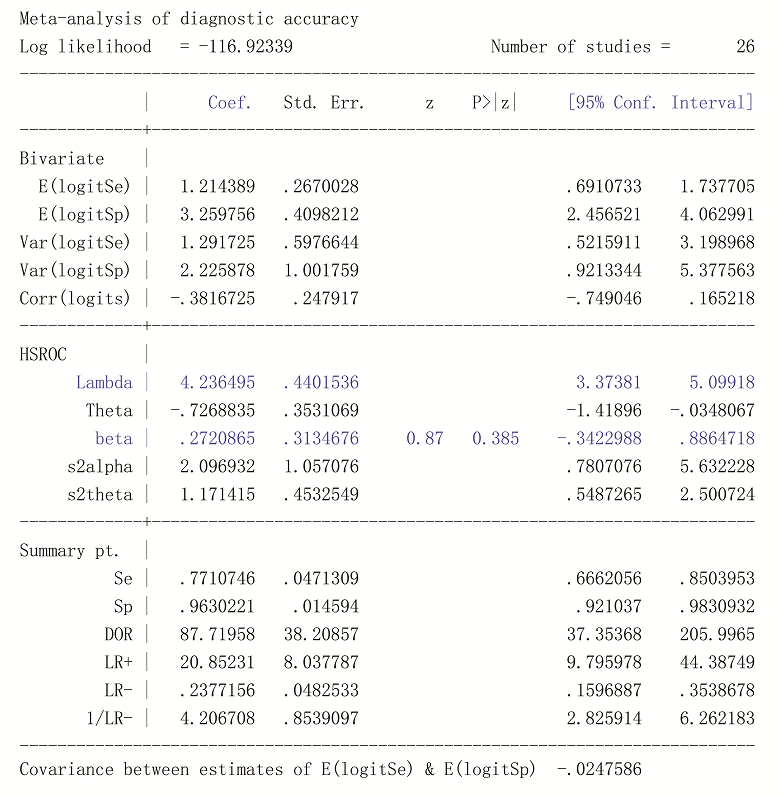
主要数字化结果如下：

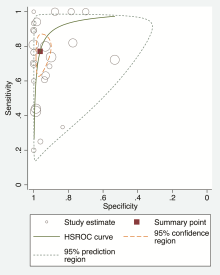
默认结果给出双变量模型和HSROC模型的参数估计（和标准误）及其近似95%可信区间、灵敏度、特异度、诊断比值比、阳性似然比、阴性似然比等诊断试验的经典指标合并量（和标准误）及其95%可信区间。HSROC模型给出的结果中, β （对应“ beta” ）估计值及其95%可信区间为0.27（-0.34, 0.89）, 且Z统计量为0.87, 相应P=0.385, 提示SROC是对称的; 反映诊断试验判别能力的效应指标（对应“ Lambda” ）的估计值及其95%可信区间为4.24（3.37, 5.10）, 提示新方法具有较高的准确性。

2.2 图示化结果

默认HSROC图中给出综合ROC图、每个研究估计及总合并量的工作点、HSROC曲线及95%可信区域、95%预测区域等, 见图1。观察95%预测区域可以发现, 用来预测敏感度和特异度之间的关系更加符合经典综合ROC 曲线形状, 其曲线图较经典方法[3]做出的曲线图更为合理。

图1 HSROC图

3 讨 论

诊断试验Meta分析面临很多挑战, 即使对一简单的2× 2格式数据进行汇总合并, 严格的统计方法也需要层次模型[6]。Rutter等[5]提出HSROC模型作为诊断试验Meta分析的基本框架, 该模型可以采用完全贝叶斯方法拟合, 但该方法没有得到广泛应用。Macaskill[7]指出应用经验性贝叶斯方法来拟合HSROC模型获得的结果与完全贝叶斯方法相似, 因其简单易行可作为一种替代方法。Chu等[8]提出对灵敏度和特异度等指标进行对数转换, 从而可以应用基本线性混合模型（generalized linear mixed model）策略来拟合模型, 其等同于Macaskill的经验性贝叶斯策略。基于Chu等[8]提出的基本线性混合模型策略, Harbord等编写了“ metandi” 包采用Stata软件通过两水平混合logistic回归模型来拟合HRSOC模型。

“ metandi” 包为Stata非官方软件包, 应用前需要进行安装：联机情况下, 在Stata软件命令行窗口键入“ ssc install metandi, replace” 即可。在10.0及以上版本Stata中, 默认“ metandi” 采用Stata内建命令“ xtmelogit” 来拟合HSROC模型, 而在8.0和9.0版本Stata中, 需要采用非官方软件包“ gllamm” 来拟合, 因此需要确认安装该软件包（安装命令： ssc install gllamm, replace）。我们的实例显示, 运用“ metandi” 包进行诊断试验的Meta分析, 可以获得不同模型的参数估计及经典指标估计, 对于HSROC模型, 至少可以获得多个水平的结果：研究水平的效应参数即每个研究的灵敏度和特异度、汇总后的灵敏度和特异度、总的灵敏度和特异度的预测分布等, 相对于经典的综合ROC方法相比, 因采用随机效应模型充分考虑了各个层次的变异, 合理考虑到敏感度和特异度之间的非线性关系; 不需要对“ 0” 格子数据加0.5进行校正等; 可以直观地得出HSROC估计图（图中可显示每个诊断试验和汇总的灵敏度与特异度估计值的均值）、HSROC估计图的95%可信区间、HSROC估计图的95%预测区域; 方法比较简便易行, 均与传统的综合ROC 方法比较更具优越性, 值得推广与应用。

在运用“ metandi” 包进行诊断试验的Meta分析要注意两点：一是如果HSROC模型中含有协变量, 则不能由metandi命令来拟合; 二是在拟合模型过程中, 使用gllamm可能会遇到“ convergence not achieved： try with more quadrature points” 、“ log likelihood cannot be computed” 等错误提示时, 要通过nip（）参数增加积分点, 如将默认的5改为7等[6]。

The authors have declared that no competing interests exist.

参考文献
[1] 余小金, 柏建岭, 荀鹏程, 等. Bayesian两变量层次模型及在断试验系统评价中的应用[J]. 循证医学, 2009, 9(6): 373-377. [本文引用:2]
[2] 祝慧萍, 方龙, 夏欣, 等. 双变量模型在诊断试验Meta分析中的应用[J]. 华中科技大学学报(医学版), 2010, 39(1): 78-81. [本文引用:2]
[3] 张天嵩, 钟文昭. Meta-DiSc软件在诊断试验Meta分析中的应用[J]. 循证医学, 2008, 8(2): 97-100, 108. [本文引用:2]
[4] Pai M, Flores LL, Hubbard A, et al. Nucleic acid amplification tests in the diagnosis of tuberculous pleuritis: A systematic review and meta-analysis[J]. BMC Infect Dis, 2004, 4: 6. [本文引用:1] [JCR: 3.025]
[5] Rutter CM, Gatsonis CA. Ahierarchical regression approach to meta-analysis of diagnostic test accuracy evaluations[J]. Stat Med, 2001, 20(19): 2865-2884. [本文引用:3] [JCR: 2.044]
[6] Harbord RM, Whiting P. Metand i: Meta-analysis of diagnostic accuracy using hierarchical logistic regression[J]. The Stata J, 2009, 9(2): 211-229. [本文引用:3]
[7] Macaskill P. Empirical Bayes estimates generated in a hierarchical summary ROC analysis agreed closely with those of a full Bayesian analysis[J]. J Clin Epidemiol, 2004, 57(9): 925-932. [本文引用:1] [JCR: 5.332]
[8] Chu H, Cole SR. Bivariate meta-analysis of sensitivity and specificity with sparse data: A generalized linear mixed model approach[J]. J Clin Epidemiol, 2006, 59(12): 1331-1332. [本文引用:2] [JCR: 5.332]