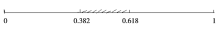作者简介:刘建萍(1966-),女,北京人,学士,从事医药学的数量化研究。
目的用药剂量在什么范围内对治疗适合?药物不良反应及病菌耐药性与剂量有关系吗?本文研究这三个问题及其关系,并寻求解决的统一之道。方法 考察剂量与用药效果的关系,以黄金区域为中段,把经验范围分成三段是研究设计的关键。结果 超大容量样本调查表明,两种药分别按公斤体重剂量由小到大给药,不良反应率都由高变低、然后再升高,呈U形规律,U形的底部出现在黄金区域上。通过黄金区域内外合理成本与不合理成本的分析,表明耐药性与用药剂量的关系也符合U形规律。结论 抗菌素被滥用、不良反应和耐药性是当今医药界的三大顽疾。用黄金区域法规定用药剂量是探讨当前解决三个难题的一个特殊突破口。
Objective What dose range in treatment is appropriate? Are adverse drug reactions and resistance related to dose? These three problems and their relationships were researched to seek solution to the road of reunification in this paper.Methods Study was conducted on the relationship between dose and drug effect, with gold zone as the middle range and empirical range divided into three sections, which are the key to the study design.Results The incidence of drug adverse reactions of both appeared U-shaped rule with dose, namely, with increase of the dose (mg·kg-1·d-1), the adverse reaction rate first decreased and then rose, and the bottom of U-shaped curve was in the gold zone. The analysis of reasonable cost and unreasonable cost indicates resistance, and the drug dose also show U-shaped rule.Conclusion Abuse of antibiotics, adverse reactions and resistance are three major medical challenges today. Utilizing the gold zone method to determine dose is the current special breakthrough in solving the three problems.
抗菌素不良反应和病菌耐药性都是药物作用于机体的坏反应, 与滥用抗菌素密切相关, 本文用黄金区域法试图解决这些问题。
大样本调查某大型儿童医院2009年用量最多的两种抗菌素, 注射用头孢孟多酯钠(Cefamandole Nafate for injection, 简称头孢孟多)177 720人次, 注射用头孢曲松钠(Ceftriaxone Sodium for injection, 简称头孢曲松)51 235人次(材料来自北京儿童医院药剂科)。上述两种药2009年全年发生的不良反应, 头孢曲松51例、头孢孟多24例(材料来自北京儿童医院向全国药品不良反应监测网络上报的信息)。这些材料包含了对药物不良反应的统计, 都是研究者事后对剂量进行分组和统计。
在指定范围0~1内, 从小到大的黄金分割点是0.618, 从大到小的黄金分割点是0.382, 这两个点之间的区域称作黄金区域[1](图1)。利用黄金区域调整用药剂量, 避免极端误差带来危害的方法称作黄金区域法[2]。
医药学在数量化研究的道路上经历了从体外研究到体内研究两个阶段。体外研究药物剂量的精准问题已经解决, 但体内研究还未达到精准水平。例如在体内, 血药浓度维持在什么样的水平治疗效果最好, 人们并不清楚。机体对药物的准确适合量不明, 是人类用药剂量的盲区。这个不明又带来两个不明:一是为了达到治疗目的, 使不良反应率控制在较低水平的剂量不明; 二是为了达到治疗目的, 使耐药性控制在较低水平的剂量不明。
考察剂量与用药效果的关系, 以黄金区域为中段, 把经验范围分成三段是研究设计的关键。
头孢孟多说明书中规定:婴幼儿治疗常规感染, 每日用药剂量按公斤体重为50~100 mg· kg-1· d-1, 这是经验范围, 其黄金区域的剂量为69.1~80.9 mg· kg-1· d-1。调查和计算情况见表1、图2。
| 表1 头孢孟多使用情况 |
对头孢孟多不同用药剂量产生的不良反应率做假设检验如下:
假设H0: P1=P2, 备择假设H1:P1≠ P2
其中P1、P2分别代表低于黄金区域与黄金区域内不良反应的总体率。
检验水平:α =0.001, 查表得临界值:
4.19> 3.29
否定H0: P1=P2, 接受 H1:P1≠ P2, α < 0.001
经U检验, 剂量低于黄金区域的不良反应率以极高度显著性高于黄金区域内的不良反应率, 检验水平α < 0.001。这是一个惊人的发现。
头孢曲松说明书中规定:婴幼儿治疗常规感染, 每日用药剂量按公斤体重为20~80 mg· kg-1· d-1, 剂量划分也是按黄金区域法进行, 调查和计算情况见表2、图3。
| 表2 头孢曲松使用情况 |
同样对头孢曲松不同用药剂量产生的不良反应率做假设检验:
经计算统计量U=3.16
检验水平:α =0.01, 查表得临界值
3.16> 2.58
否定H0: P1=P2, 接受 H1:P1≠ P2, α < 0.01
惊人的发现再次出现, 剂量低于黄金区域的不良反应率以高度显著性高于在黄金区域内的不良反应率, 检验水平α < 0.01。
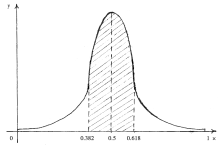
由于机体对药物的准确适合量是一个盲区, 它受到生理、病理复杂过程的众多因素影响, 而这么多因素可以看做是互相独立的, 每一个因素都起不到绝对主导作用, 根据中心极限定理, 准确适合量作为随机变量可以认为它服从正态分布。
图4是正态分布的概率密度函数y=f(x)=
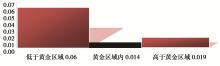
本文对头孢孟多和头孢曲松治疗常规感染的门诊患儿进行了超大容量的样本调查, 这个调查也可以认为是对全社会的抽样调查。两种药剂量在黄金区域内不良反应率都是最低的(0.014%和0.034%); 两种药剂量高于黄金区域不良反应率分别增高(0.019%和0.043%), 具有共同的规律性。令人吃惊的是, 用药剂量小于黄金区域的不良反应率, 两种药都显著增高(0.06%和0.344%), 也都具有共同的规律性, 而且表现更加强烈, 分别是黄金区域内不良反应率的4倍多和10倍多。考察两种用量最多的抗菌素不良反应的规律具有一致性, 不良反应率的变化走向都呈现U形, 即随着按公斤体重剂量由小到大给药, 不良反应由高变低, 然后再升高。剂量控制在黄金区域内不良反应率最低, 处于U形底部。
只要使用抗菌素, 病原菌就会产生耐药性, 耐药性与使用抗菌素如影随形。但是为了治疗一些感染性疾病, 很多情况必须使用抗菌素, 这是回避不了的矛盾。在剂量合理的范围内用药产生的耐药性是必须付出的成本, 可以称之为合理成本。不合理的成本是产生更多耐药性的成本, 表现为两个极端。一是抗菌素使用剂量过多, 抗菌素使用越多, 产生耐药性越快, 过多部分没有积极作用, 只有消极作用, 其效果不仅导致菌群失调, 也使得继续使用该药物时必须再加大剂量, 导致药量越来越多, 药品级别越来越高。二是过少使用抗菌素或用用停停, 这样做使得没有被杀灭的细菌适应新环境, 继续繁殖, 抗药能力更加顽强, 为了达到治疗目的, 下一阶段用药时, 必须比常规用药剂量更大才能杀灭病菌。这两个极端都会付出更多的成本, 是不合理成本。
用药剂量过高过低都要付出不合理成本, 产生较强的耐药性, 这符合U形规律, 耐药性较低的剂量在中段。要保证用药剂量最好, 中段取法必须满足两条原则:避免剂量过低或过高; 以较大的概率保证疗效。在图4中, 黄金区域对应的曲线段是全凸的, 这段上面包含了“ 面积大肚” , “ 大肚” 的面积即概率集中了全部概率的70%。区域缩小一点点, 面积就会失去很多, 因为它在“ 大肚” 内; 区域扩大很多, 面积并没有增加多少, 因为它在“ 大肚” 外, 只有黄金区域同时满足这两个原则。所以黄金区域是克服耐药性盲区的最好选择。
抗菌素被滥用、不良反应和耐药性是当今医药界的三大顽疾。关于不良反应和耐药性, 国内外传统研究都是在生理、病理和药理上找原因, 原因复杂多样, 个体差异大, 难于发现规律。我们用黄金区域法研究剂量的作用, 在理论上总结出黄金区域内给药的两大优势:
第一, 在不到经验范围1/4的黄金区域内包含机体对药物的准确适合量的概率将近70%, 这对于解决用药剂量的盲区问题至关重要;
第二, 抗菌素不良反应和病菌耐药性与用药剂量有关, 并且呈U形规律, 在经验范围的黄金区域内用药, 两方面的坏反应都达到了最低, U形的底部出现在黄金区域上。
用黄金区域法确定剂量范围, 可以保证疗效, 可以减少抗菌素不良反应和降低病菌耐药性, 简便实用, 是当前探讨解决三个难题的特殊突破口。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|