引用本文
张天嵩, 熊茜, 袁婷. 附加轮廓线漏斗图的绘制在R软件中的实现. 循证医学, 2013,13(5): 307-309
ZHANG Tian-song, XIONG Qian, YUAN Ting. Drawing Contour-Enhanced Funnel Plot in R Software. Journal of Evidence-Based Medicine,2013, 13(5): 307-309  
Permissions
Copyright©2013 《循证医学》杂志 版权所有
附加轮廓线漏斗图的绘制在R软件中的实现
张天嵩a,b, 熊茜a, 袁婷a
上海市静安区中心医院 a. 科教部, 上海 200040
上海市静安区中心医院 b. 中医科, 上海 200040

作者简介： 张天嵩（1970-）,男,山东昌邑人,医学博士,主任医师,副教授,从事呼吸系统疾病中西医结合临床及循证医学方法学研究。

摘要

目的介绍附加轮廓线漏斗图在R软件中的实现及应用。方法对实例中的数据采用R软件 “meta”扩展包的funnel（）和trimfill（）函数绘制附加轮廓线漏斗图,并判断缺失研究分布的区域。结果通过观察附加轮廓线漏斗图,可以发现存在不对称,缺失数据分布在无统计学显著性区域,表明存在发表偏倚。结论附加轮廓线漏斗图可以用来帮助判断漏斗图不对称是发表偏倚还是其他原因导致。

关键词: 附加轮廓线漏斗图; Meta分析; R软件
中图分类号:R195.1 文献标识码:A
Drawing Contour-Enhanced Funnel Plot in R Software
ZHANG Tian-songa,b, XIONG Qiana, YUAN Tinga
a. Department of Science & Education
b. Department of TCM, Jing’an District Central Hospital, Shanghai 200040, China
Abstract

Objective To introduce how to draw a contour-enhanced funnel in R software and its application in meta-analysis.Methods It was illustrated on an example data to draw a contour-enhanced funnel by using funnel（） function and trimfill（） function in meta package in R software, and to perceive the missing studies in areas of statistical significance from the plot.Results The contour-enhanced funnel was asymmetry, and the studies seem to be missing in areas of non-significance, and it was explained that funnel plot asymmetry may be due to publication bias.Conclusions Contour-enhanced funnel could be used to help distinguish publication bias from other cause of funnel plot asymmetry.

Key words: contour-enhanced funnel plot; meta-analysis; R software

在过去的25年中,Meta分析作为一种汇总多个研究结果而进行总体效应评价的科学研究方法,已广泛应用于社会和医学科学研究中[ 1],检验并解释发表偏倚在Meta分析中占重要地位[ 2], 通过评价漏斗图是否存在不对称是识别发表偏倚的常用方法[ 3],但发表偏倚不是引起漏斗图不对称的唯一原因,任一与研究效应和研究样本真正相关的影响因素均可导致漏斗图的不对称,如低质量方法学设计的小样本研究等[ 4, 5],而且常规的漏斗图不能鉴别其不对称的原因,Peters等在2008年提出一种附加轮廓线漏斗图（contour-enhanced funnel plots）来帮助判断漏斗图的不对称是由发表偏倚还是由其他原因引起[ 4]。近年来,经统计学家的努力,该方法可由Stata、R等软件实现[ 6, 7],本文以实例说明,用Schwarzer 为R15.1编写的“meta”扩展包来绘制附加轮廓线漏斗图的具体过程,并阐述其应用。R软件及“meta”扩展包的下载及安装可以参照文献方法[ 8]。

1 资料和方法
1.1 数据来源

数据来源于公开发表的文献[ 9]：观察糖蛋白Ⅱb/Ⅲa抑制剂治疗ST段抬高心肌梗塞的效果,纳入11个研究共1 634名患者,含阿昔单抗（Abciximab）、替罗非班（Tirofiban）、依替巴肽（Eptifibatide）三种药物,观测终点为达到梗塞相关血管心肌梗塞溶栓血流分级3级。

1.2 绘制附加轮廓线漏斗图的具体方法

1.2.1 建立数据集

主要使用data.frame（）函数,以数据框方式,在R软件中建立一个数据集,将文献中的数据输入,并命名为“mydata”,命令如下：

>study <-c（"RELAx-AMI 2007", "ERAMI 2006", "REOMOBILE 2004", "Rakouski 2007", "Reopro-BRIDGING 2004","Zomorman 2002", "Emre 2006", "Cutlip 2003", "On-TIME 2004", "INTAMI 2005","On-TIME 2006"）

>early.event<-c（25, 7, 11, 8, 8, 9, 10, 7, 46, 18, 41）

>early.total<-c（105,40,48,25,28,56,32,23,243,53,171）

>late.event<-c（11,5,8,3,2,1,4,6,36,5,27）

>late.total<-c（105,40,52,30,27,56,35,30,244,49,142）

>mydata<-data.frame（study, early.event, early.total, late.event, late.total）

>names（mydata） <-c（"sutdy", "early.event", "early.total", "late.event", "late.total"）

在R软件命令行操作窗口键入“mydata”可查看具体数据（略）,其中“sutdy”表示研究名称,“early.event”、“early.total”、“late.event”、“late.total”分别表示每个研究中早期和晚期应用糖蛋白Ⅱb/Ⅲa抑制剂治疗心肌梗塞溶栓出现事件的人数及研究总人数。

1.2.2 绘制传统漏斗图并进行不对称检验

先用R软件绘制传统漏斗图,并进行不对称检验,命令如下：

>library（meta）

>mymeta <-metabin（early.event, early.total, late.event, late.total, data=mydata, studlab= study, comb.random=TRUE, sm="OR", method="I"）

>funnel（mymeta）

>metabias（mymeta）

上述命令是载入meta扩展包,并采取meta包中metabin（）函数进行Meta分析,其主要参数有：OR为效应指标,选取随机效应模型,采用“Inverse”法合并效应量;以funnel（）函数绘制传统漏斗图;以metabias（）函数中的“Harbord”法进行漏斗图的不对称检验。

1.2.3 绘制附加轮廓线漏斗图及剪补后的附加轮廓线漏斗图

首先,用funnel（）函数绘制附加轮廓线漏斗图,命令如下：

>funnel（mymeta, comb.random=TRUE,level=0.95, contour=c（0.9, 0.95, 0.99）, col.contour =c（"darkgray", "gray", "lightgray"））

>legend（4,0.1,c（"0.1 > p > 0.05", "0.05 > p > 0.01", "< 0.01"）, fill=c（"darkgray", "gray", "lightgray"））

>par（oldpar）

其次,结合trimfill（）函数和funnel（）函数绘制剪补后附加轮廓线漏斗图,命令如下：

>mytrimfill <- trimfill（mymeta）

>funnel（mytrimfill, comb.random=TRUE,level=0.95, contour=c（0.9, 0.95, 0.99）, col.contour=c（"darkgray", "gray", "lightgray"））

>legend（3.2,0.1,c（"0.1 > p > 0.05", "0.05 > p > 0.01", "< 0.01"）, fill=c（"darkgray", "gray", "lightgray"））

>par（oldpar）

2 结 果
2.1 传统漏斗图绘制及不对称检验结果

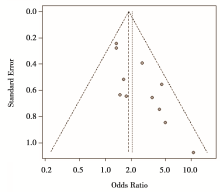
传统漏斗图如 图1所示,从视觉来看,漏斗图左下底部明显“缺角”;采用“Harbord”法进行漏斗图的不对称检验, P=0.011 84,说明漏斗图存在明显不对称。

图1 传统漏斗图

2.2 附加轮廓线漏斗图及剪补后附加轮廓线漏斗图的绘制结果

图2 附加轮廓线漏斗图

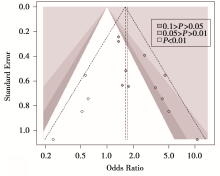
对比附加轮廓线漏斗图（ 图2）和传统漏斗图（ 图1）,可以发现两者的主要区别是：附加轮廓线漏斗图增加了代表统计显著性 P>0.05、0.1> P>0.05、0.05> P>0.01、 P<0.01的区域,分别为白色、深灰色、灰色和银灰色,所在研究都分布在右边,有6个研究分布在有统计学意义区域（灰色和银灰色区域）,有5个研究分布无统计学意义区域（白色区域）;结合剪补后的附加轮廓线漏斗图（ 图3）,需要补4个缺失的研究,而且该4个研究分布在无统计学意义区域（白色区域）,说明有无统计学意义的研究未发表,提示该Meta分析存在发表偏倚。

图3 剪补后附加轮廓线漏斗图

3 讨 论

传统漏斗图是Meta分析中应用多个研究数据做成的散点图,以效应量大小为横坐标,以效应值的权重如标准误、方差倒数或样本量等为纵坐标[ 10],最常用的是标准误[ 11]。附加轮廓线漏斗图的绘制与传统漏斗图相同,但在传统漏斗图基础上,增加了识别统计学显著性（如0.01、0.05、0.1）水平相对应的轮廓线[ 4],这些轮廓线将漏斗分成了不同统计学显著性的区域,如 图2和 图3中的白色、深灰色、灰色和银灰色区域,从而以利于识别出绘制在漏斗图上的点是否具有统计学显著性;判断是否存在不对称;如果存在不对称,结合剪补法,发现缺失的研究分布位置,从而分析漏斗图不对称产生的原因是发表偏倚还是其他原因。

如果附加轮廓线漏斗图呈现“漏斗样”形状：效应量的精度随着样本量的增加而增加,其宽度随精度的增加而逐渐变窄,最后趋近于点状[ 12];也就是说样本量小的研究,数量多、精度低,分布在漏斗图的底部呈左右对称排列;样本量大的研究,精度高,分布在漏斗图的顶部,且向中间集中[ 3],说明不存在发表偏倚[ 12]。

如果存在不对称,且缺失的研究分布在无统计学显著性区域（如 图2中白色区域）,则说明由发表偏倚导致漏斗图不对称[ 4],尽管还有其他解释[ 12];如果存在不对称,且缺失的数据分布在有统计学显著性区域（如 图2中的深灰色、灰色和银灰色区域）,则说明不对称可能由其他原因而非发表偏倚导致[ 8, 12]。

Stata软件中“confunnel”命令和R软件的“meta”和“metafor”扩展包都能够实现附加轮廓线漏斗图的绘制,但R为开源软件,其“meta”和“metafor”扩展包绘制出的附加轮廓线漏斗图精美直观;此外,为避免将“漏斗图不对称等同于发表偏倚”的错误,建议系统评价者在做Meta分析时使用R软件绘制附加轮廓线漏斗图判读漏斗图不对称是由发表偏倚还是由其他因素引起。

The authors have declared that no competing interests exist.

参考文献
[1] Huedo-Medina TB, Sanchez-Meca J, Matin-Martinez F. Assessing heterogeneity in meta-analysis: Q and I2 index?[J]. Psychoi Methods, 2006, 11(2): 193-206. [本文引用:1]
[2] Haidich AB. Meta-analysis in medical research[J]. Hippokratia, 2010, 14(Suppl 1): 9-37. [本文引用:1] [JCR: 0.589]
[3] 张天嵩, 钟文昭, 徐同成. 漏斗图的绘制与不对称检验在Stata中的实现[J]. 循证医学, 2009, 9(2): 110-114. [本文引用:2]
[4] Peters JL, Sutton AJ, Jones DR, et al. Contour-enhanced meta-analysis funnel plots help distinguish publication bias from other causes of asymmetry[J]. J Clin Epidemiol, 2008, 61(10): 991-996. [本文引用:3] [JCR: 5.332]
[5] Higgins JPT, Green S(eds). Cochrane hand book for systematic reviews of interventions. Version 5. 1. 0[updated March 2011], [EB/OL]. http://www.cochrane-handbook.org [本文引用:1]
[6] Palmer TM, Peters JM, Sutton AL, et al. Contour-enhanced funnel plots for meta-analysis[J]. Stata J, 2008, 8(2): 242-254. [本文引用:1] [JCR: 1.31]
[7] Schwarzer G. Package ‘meta’[EB/OL]. http://cran.r-project.org/web/packages/meta/meta.pdf, 2012-11-29. [本文引用:1]
[8] 张天嵩, 钟文昭. 实用循证医学方法学[M]. 长沙: 中南大学出版社, 2012: 352-379. [本文引用:2]
[9] de Luca G, Gibson CM, Belland i F, et al. Early glycoprotein Ⅱb-Ⅲa inhibitors in primary angioplasty (EGYPT) cooperation: An individual patient data meta-analysis[J]. Heart, 2008, 94(12): 1548-1558. [本文引用:1] [JCR: 5.014]
[10] Lau J, Ioannidis JP, Terrin N, et al. The case of the misleading funnel plot[J]. BMJ, 2006, 333(7568): 597-600. [本文引用:1]
[11] Sterne JA, Egger M. Funnel plots for detecting bias in meta-analysis: Guidelines on choice of axis[J]. J Clin Epidemiol, 2001, 54(10): 1046-1055. [本文引用:1] [JCR: 5.332]
[12] Ahmed I, Sutton AJ, Riley RD. Assessment of publication bias, selection bias, and unavailable data in meta-analyses using individual participant data: A database survey[J]. BMJ, 2011, 344: d7762. [本文引用:4]