大多数Meta分析在估计相关系数时,由于各个相关系数的方差过于依赖相关性^[1]42,故不直接使用相关系数的值,而是先进行Fisher’s z转换,经过Fisher’s z转换后,其值的分布随着样本量增大趋于正态分布。Fisher’s z转换的公式为：

z = 0.5 × ln（ 1+r1-r）（1）

根据每个研究的样本量ni,分别给予不同的权重wi,得到合并的 z值,其公式为：

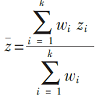（2）

权重wi=ni-3,效应值的标准误为

S_E= 1∑Wi

Meta分析在合并效应值之前,首先要明确研究间是否存在异质性,即各研究结果的变异是否由随机误差引起^{[ 2]}。可以采用 Q检验,其公式为：

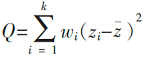
Q统计量服从自由度为k-1（k为纳入Meta分析的文献数）的卡方分布,如果 Q < Xk-1,0.052,表明 P > 0.05,同类研究间的异质性由抽样误差造成的,可选用固定效应模型,合并的效应值公式采用上述公式（2）;如果 Q≥ Xk-1,0.052,则 P≤0.05,可认为同类研究具有异质性,再对异质性原因进行处理,若异质性原因分析且处理后仍无法解决异质性时,可选用随机效应模型,权重调整为： wi*=（ wi-1- h）^-1,其中

h= Q-k+1∑Wi-∑wi2/∑wi

合并的效应值公式为：

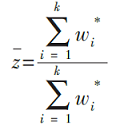
对计算出的合并效应值是否为零进行统计推断。Hedges的合并效应值显著性检验公式为^[1]42-72：

z̅=z̅SE

评价Meta分析中纳入的研究是否存在“发表偏倚”是进行Meta分析的一项预备性工作^{[ 3]}。评价“发表偏倚”有多种方法,如定性法有“漏斗图”、“森林图法”,定量方法有Begg’s 检验、Egger’s 检验和Macaskill’s 检验等。本研究以实例数据编写的是Begg’s 检验的SAS程序。

以我们之前研究的课题内容为例,对人格特征与抑郁关系的研究结果进行定量的综合评价。 表1为该课题研究的纳入的部分文献数据。

表1

表1

表1 纳入文献的一般情况

表1 纳入文献的一般情况

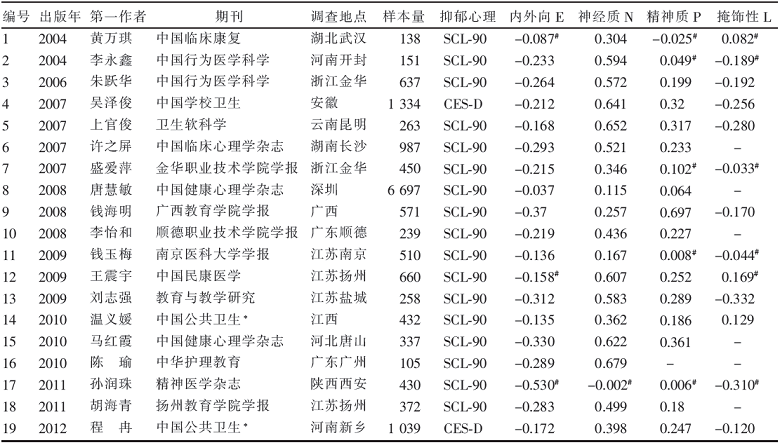
以内外向性因子E与抑郁之间的相关系数数据为例。

data a;

input ni ri@@;

zi=0.5^*LOG((1+ri)/(1-ri));/^*z转换^*/

wi=ni-3;/^*权数^*/

s_num=18;

cards;

138 -0.087 151 -0.233 637 -0.264 1334 -0.212

263 -0.168 987 -0.293 450 -0.215 571 -0.37

239 -0.219 510 -0.136 660 -0.158 258 -0.312

432 -0.135 337 -0.33 105 -0.289 430 -0.53

372 -0.283 1039 -0.172

;

data b; set a;

wi2=wi^**2; wizi=wi^*zi; wizi2=wi^*zi^**2;

swi1+wi; swi21+wi2; /^*计算合计权数^*/

swizi1+wizi; swizi21+wizi2;

Id=_n_;

if _n_=s_num then do;

swi=swi1; swi2=swi21;

swizi=swizi1; swizi2=swizi21;

zwbar=swizi/swi;/^*zwbar为平均效应量^*/

se1=1/swi^∗∗0.5;/^*效应值的标准误^*/

Q=swizi2-zwbar^**2^*swi;/^*异质性检验Q统计量^*/

smu2=(Q-s_num+1)/(swi-swi2/swi);

end;

P=1-probchi(Q,s_num-1);/^*异质性检验的p值^*/

proc sort;

by descending Id;

data c; set b;

fr1=(exp(2^*zwbar)-1)/(exp(2^*zwbar)+1);

frlow=(exp(2^*(zwbar-1.96^*se1))-1)/(exp(2^*(zwbar-1.96^*se1))+1);

frup=(exp(2^*(zwbar+1.96^*se1))-1)/(exp(2^*(zwbar+1.96^*se1))+1);

/^*frlow、frup分别为固定效应模型的相关系数r的95%置信区间^*/

smu2s+smu2;

wis=1/(wi^**(-1)+smu2s);/^*权数调整值^*/

wiszi=wis^*zi;

swis1+wis; swiszi1+wiszi;

if_n_=s_num then do;

swis=swis1; swiszi=swiszi1;

zbar=swiszi/swis;/^*调整权数后平均效应量的计算^*/

se2=1/swis^**0.5;/^*sy2为效应量加权均数的标准误^*/

z=zbar/se2;/^*合并效应量的假设检验^*/

p_z=1-probnorm(abs(z));

fr2=(exp(2^∗zbar)-1)/(exp(2^∗zbar)+1);/^*将平均效应量z转化为r值^*/

rlow=(exp(2^*(zbar-1.96^*se2))-1)/(exp(2^*(zbar-1.96^*se2))+1);

rup=(exp(2^*(zbar+1.96^*se2))-1)/(exp(2^*(zbar+1.96^*se2))+1);

/^*rlow、rup分别为随机效应模型的相关系数r的95%置信区间^*/

end;

proc print;

run;

data d;

set b;

/^* 产生 egger’s 检验用应变量 y 和自变量 x^*/

egger_y=zi/(wi^**0.5)^**(-1);

egger_x=1/(wi^**0.5)^**(-1);

/^* egger’s 检验程序^*/

proc reg;

model egger_y=egger_x;

run;

原文研究中经过敏感性分析,第8篇文章对内外向E、神经质N、精神质P与抑郁相关性影响较大,第4篇和第12篇对掩饰性L因子与抑郁相关性影响较大,故不纳入分析。

剔除有关文献后,重新进行异质性检验, P<0.05,故采用随机效应模型进行合并效应量估计,结果见 表2,跟原文的研究结果（用RevMan 5.0和STATA 11.0软件进行的统计分析）非常接近,原文的结果见 表3。

表2

表2

表2 人格特征与抑郁相关性异质性检验、合并效应估计及发表偏倚检验（SAS分析结果）

表2 人格特征与抑郁相关性异质性检验、合并效应估计及发表偏倚检验（SAS分析结果）

表3

表3

表3 人格特征与抑郁相关性异质性检验、合并效应估计及发表偏倚检验（原文分析结果）

表3 人格特征与抑郁相关性异质性检验、合并效应估计及发表偏倚检验（原文分析结果）