作者简介:马兴华(1985-),男,回族,新疆沙湾人,硕士研究生,从事统计学方法及其医学应用研究。
正态分布是一种重要的连续型概率分布。统计分析中,研究者们时常跳过了对所研究变量的正态性检验,直接认为资料满足正态假定。如果恰逢涉及的数值变量并非来自正态总体,就会得到错误的分析结果。常用的正态性检验方法主要有两大类:一是主观判断的图示方法,二是客观量化的统计指标计算辅以检验。本文介绍常见的几种正态性检验方法,为数值变量统计学分析方法的正确运用提供参考。
Normal distribution is one of the important distributions for continuous variables. In many statistical analyses, researchers often assumed directly the data were normally distributed without test before hand. If the numerical variables are not normally distributed, it may lead to wrong results. Normality tests which are commonly used can be classified into two categories. One category includes subjective graphical methods, and the other category contains computational methods including hypothesis tests which are objective and quantitative. In this paper, several normality tests popularly used will be introduced according to the above two categories to provide references for proper applications of statistical analyses of numerical variables.
正态分布又叫高斯分布,“正态”即“对称的状态”,本意是说如果在观察或试验中不出现重大失误,则结果应遵循这种模式的分布——尽管随着人们实践经验的积累发现事实并非如此。正态分布之所以得到普遍重视,除了它可以用来刻画数值变量的分布特征外,另一个重要原因要归功于Fisher及其同时代的若干杰出学者。他们对正态分布下一系列重要的统计量建立了形式简约且在计算上可行的小样本理论,为统计推断提供了极大的方便,而在非正态的情况下则没有可比拟的结果[ 1, 2]。基于此,人们在实际统计分析时,总是乐于采用正态假定。人们在对一个数值变量进行分析之前,可以参照既往基于大样本所推测的变量分布形式,确定正态性假定的合理性。然而,有时既往文献中没有基于大样本的变量分布形式定论,致使研究者对正态性假定是否合理无充分的把握。这时就只好基于实际的观测数据,实施正态性检验。
统计分析包括统计描述和统计推断[ 1],正态性分析主要有统计图绘制、统计指标计算并辅以检验两种方法。利用统计图可以直观地呈现变量的分布,同时还可以呈现出经验分布和理论分布的差距。峰度、偏度就是两个常用的正态性统计描述指标,通过构建检验统计量还能实现正态性检验, 表1中列出了构建检验统计量对样本进行正态性检验的主要常用方法。
| 表1 数值变量正态性检验的常用方法 |
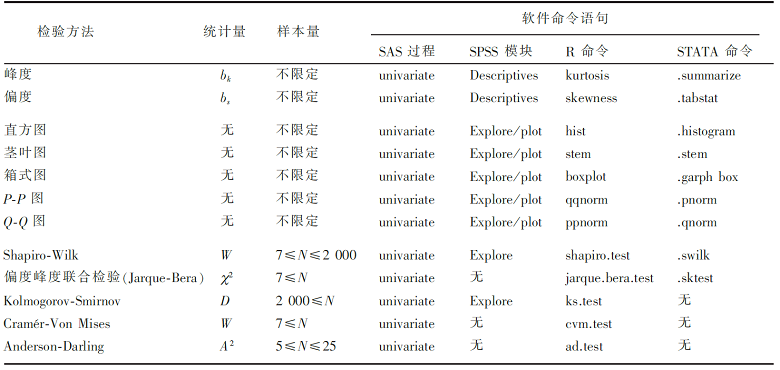
如 表1所示,直方图、茎叶图和箱式图为借助图形形式描述分布特征的统计方法,而统计描述指标峰度和偏度是借助数值计算的形式描述分布特征的统计方法。基于理论分布假定的概率图、 P−P图、 Q−Q图为借助图形来考察正态性的统计方法,常用的统计软件如SAS、SPSS、R、STATA均有相关命令或者过程步骤基于样本数据的正态性检验, 表2给出了这4种统计软件实现正态性检验方法的命令语句,以及各种方法对样本量的要求。
| 表2 各种数值变量正态性检验方法的统计量及软件实现 |
为更好地对比分析各种正态性检验方法,以三组常见的医学数据为例进行阐述。 图1(a)为2012年在某市随机调查的200例正常成年人血铅含量(10 mg/kg)的频率密度直方图; 图1(b)为2012年某省农村120例6~7岁正常男童胸围(cm)测量值的频率密度直方图; 图1(c)为2012年某地150例正常成年人心率(bpm)的频率密度直方图。
统计图形法中既有不基于任何分布假定的一般统计描述方法,也有基于正态分布假定的正态性考察方法,前者主要是呈现当前样本数据的内部信息,后者则需考虑样本所对应的理论分布是否服从(或近似)正态分布。
2.1.1 不基于任何分布假定的统计图
直方图、茎叶图和箱式图常用于统计描述。当样本量很大时,组段可以分得很细,频率直方图的包络线越来越接近总体的密度函数曲线[ 2]。如果这时把频率直方图与正态分布的概率密度函数曲线相比,可以直观地呈现正态逼近效果。茎叶图的用途同直方图,它不仅具备与直方图相同的直观性,同时能精细表达样本数据的取值水平,当样本量小时,可以通过茎叶图进行正态性呈现[ 1, 3]。箱式图主要用于多组数据平均水平和变异程度的直观比较,每一组数据均可呈现其最小值、 QL、 M、 QU、最大值,如果一组数据服从正态分布,其 QL和 QU应呈关于 M对称[ 1, 3]。
图1(a)频率密度直方图的密度曲线明显偏态,可初步判断样本所对应的总体不服从正态分布; 图1(b)和 图1(c)频率密度直方图的密度曲线呈中间高、两边低、左右基本对称的“钟形”曲线,提示两组样本所对应的总体近似服从正态分布。
2.1.2 基于正态分布假定的统计图
概率纸法是一种经典的数据分布特征考察方法,是早期手工计算时代研究者的首选方法。正态概率纸能使由正态变量的取值 x和相应的分布函数 F( x)组成的数对( x, F( x))在概率纸上呈一条直线,其线性度是判断正态性的依据[ 2]。
计算机出现后使得繁复计算可以便捷实现。 P−P图是根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图,用于直观地考察样本数据是否服从某一概率分布[ 4]。如果样本数据服从所假定的分布,则散点较好地落在原点出发的45° 线附近。 Q−Q图的结果与 P−P图相似,只是 P−P图是用概率分布的累计比进行正态性考察,而 Q−Q图是用概率分布的分位数进行正态性考察[ 4]。同 P−P图一样,如果样本数据对应的总体分布确为正态分布,则在 Q−Q图中,样本数据对应的散点应基本落在原点出发的45° 线附近。
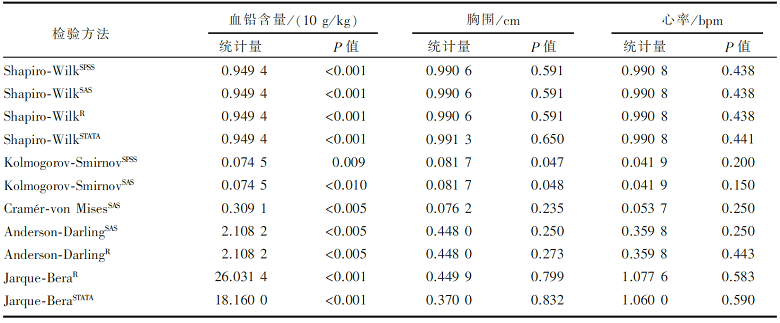
利用统计图判定样本数据的正态性很难避免分析者个人的主观性[ 2],于是人们尝试构造统计指标进行正态性分析的统计描述与推断。 表3为借助不同统计软件对 图1中三组实例数据计算出的正态性统计指标,下面将结合软件输出的统计指标检验结果简单介绍各种检验方法并做对比分析。
| 表3 正常成年人血铅含量、正常男童胸围和正常成年人心率正态性检验结果 |
2.2.1 基于偏度系数和峰度系数的正态性检验方法
理论上,正态分布的偏度系数为0,峰度系数为3,利用正态分布的这两个特性可以检验样本数据所来自总体的正态性。
2.2.1.1 偏度系数检验
偏度系数用于刻画数据的对称性,关于均值对称的数据其偏度系数为0,正侧拖尾(较负侧)更严重时偏度系数为正值,负侧拖尾(较正侧)更严重时偏度系数为负值。利用样本观测值 x1, x2,…, xn估计偏度系数的公式为 bs = 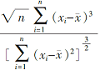
2.2.1.2 峰度系数检验
利用样本观测值 x1, x2,…, xn计算峰度系数的公式为 bk = 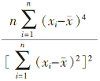
在计算出偏度系数 bs和峰度系数 bk后,后续的假设检验通常采用单侧检验法[ 2]。文献中偏度系数与峰度系数的界值表只间断地给出样本量7≤ N≤5 000对应的界值,没有给出的界值只能靠近似法。
2.2.1.3 偏度峰度联合检验(Jarque−Bera检验)
单独使用偏度系数检验或峰度系数检验都具有前提假定,例如,单独使用峰度系数检验时,资料被假定满足正态分布应有的对称特征,反之亦然。如果对资料的偏度和峰度均不能确定是否偏离正态分布,应使用偏度峰度联合检验。为偏度峰度联合检验构造的联合统计指标为 Y2 = X2( bs) + X2( bk),其中 X( bs)和 X( bk)分别是作Johnson SU变换后的近似标准正态变量[ 2],偏度峰度联合正态性检验也需要结合界值表做出统计推断,目前文献中作者通过线性插值法给出样本容量20≤ N≤1 000 对应的界值。顺便指出, Y2近似服从自由度为2的 χ2分布[ 2]。
联合考虑偏度和峰度的另一种正态性检验方法是Jarque−Bera检验,构造的统计指标为 JB= ( b+( bk-3)2。如果样本数据所来自的总体服从正态分布, 则 JB近似服从自由度为2的χ2分布。而 表3的实例结果显示,Jarque−Bera检验相比于其他检验方法更容易成功地接受正态性假定,即Ⅰ类错误风险较低。
2.2.2 Shapiro−Wilk正态性检验( W检验)
Shapiro−Wilk正态性检验法[ 2]由Shapiro和Wilk 1965年提出的,又称 W检验,一般样本量50≤ N≤100时采用Shapiro−Wilk正态性检验,而在SAS软件中当样本量7≤ N≤2 000时,一律只报告Shapiro−Wilk正态性检验结果。鉴于本法目前被广泛采用,目前多数统计软件都能实现,此处给出完整的分析步骤。
建立检验假设 H0: 样本数据所来自的总体服从正态分布,后续步骤为:
(1)将 n个样本观测值按由小到大的次序排列: x(1)≤ x(2)≤… x(i)≤…≤ x( n)
(2)计算Shapiro−Wilk正态性检验统计指标:
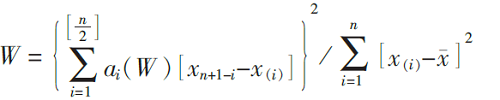
其中 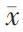
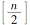
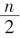
(3)根据给定的检验水准α和样本容量 n查统计指标 W的界值表得到 Wα;
(4)做出统计推断:若 W< Wα,则拒绝 H0,认为样本数据所来自的总体不服从正态分布;若 W>Wα,则不拒绝 H0。
2.2.3 Kolmogorov−Smirnov( K−S)正态性检验
Kolmogorov−Smirnov( K−S) 检验是一种基于经验分布函数的检验方法[ 2],若总体分布函数 F( x)未知,但有样本观测值 x1, x2,…, xn,则把样本中 n个观测值按从小到大的次序排列成 x(1)≤ x(2)≤… x(i)≤…≤ x( n),可以得到经验分布函数:
Fn( x) = 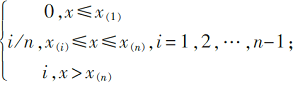
根据Glivenko−Cantelli定理,当 n很大时,由样本观测得到的经验分布函数 Fn( x)是总体分布函数 F( x)的良好近似。1933年Kolmogorov提出了检验统计指标 Dn ,1948年Smirnov给出了用于估计 Dn经验分布的拟合度表。统计指标 Dn的具体形式为:
Dn = 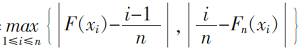
鉴于目前统计软件SPSS被广大医学工作者普遍使用,这里特别强调指出,SPSS中Kolmogorov−Smirnov检验法有两种实现方式[ 4],方式一是分析模块中的探索(Explore Plot)选项,方式二是非参数检验模块中的单一样本Kolmogorov−Smirnov检验;方式一的检验结果右上角常有一个 a注释号,表示经过校正后的Kolmogorov−Smirnov检验结果,它适用于一般的正态性检验。而方式二的非参数检验结果没有经过校正,这种检验方式只能推断资料是否服从标准正态分布。实际应用中若出现两种检验方式结论不一致,一般以方式二的结果为准。
利用统计软件R进行Kolmogorov−Smirnov正态性检验时,特别要求检验样本中不能出现相同值,原因是R软件进行正态性检验时要求检验样本连续,而连续分布出现相同值的概率为0,如果出现相同值,可对其一加上一个充分小的数值。
另外,Kolmogorov−Smirnov 检验能检验样本所代表的总体分布的正态性,也能检验样本所代表的总体是否服从其他分布,该法具有“通用性”。相对于其他方法而言,此法的正态性检验效率偏低,也最容易受样本含量和异常值等因素的影响[ 2]。
2.2.4 Cramér−Von Mises 检验
1928年Cramér−Von Mises定义了另一种基于经验分布函数的正态性检验统计指标 W2:
W2 = n 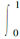
式中 Fn( x)表示由样本观测得到的经验分布函数, F( x)表示总体分布函数。
实际应用中Cramér−Von Mises 检验比Kolmogorov−Smirnov 检验更容易拒绝正态分布假定( 表3)。需要注意的是应用统计软件R的nortest程序包做Cramér−Von Mises正态性检验时要求样本量 N≥7。
2.2.5 Anderson−Darling检验
1954年Anderson−Darling提出正态性检验统计指标 A2:
A2 = -n - 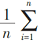
式中 Fn( x)表示由样本观测得到的经验分布函数, F( x)表示总体分布函数。
当总体分布参数未知,而样本量小到5≤ N≤25范围的情况下,Anderson−Darling检验依旧可以较好地实现正态性检验,能敏感地揭示资料潜在的不对称性。统计软件SAS和R的ADGofTest程序包可以报告相应的检验结果[ 5]。
正态分布作为一种重要的连续型概率分布,在统计学中占有重要地位。统计学中一系列重要的统计指标的建立均基于正态假定。在实际应用中,如果既往的大样本资料已经提示某医学观测指标服从正态分布,那么课题组在处理这个指标时,可以直接采用正态假定前提;而不提倡无视既往经验,由后续研究人员基于各自资料反复对这个指标做正态性考察。如果既往权威文献对所研究指标的分布模式确实没有定论,方需课题组利用获得的观测数据(有时要先施行变量变换)去探明。
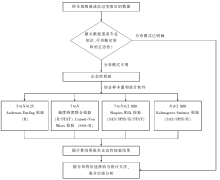
统计图形方法可直观判断样本所对应的总体分布模式,但这类方法难免个人判断的主观性。基于统计指标计算的正态性检验方法比统计图形方法更加客观,本文简要介绍了常用的几种基于统计指标的正态性检验方法及这些方法在统计软件中的实现方式,具体分析时可参考如下流程图( 图2)。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|