作者简介:周权(1987-),男,湖南常德人,医师,医学硕士,从事循证医学方法学研究。
]SAS被誉为国际上数据处理和统计分析领域的标准软件系统,其程序编写复杂且难度较大,对使用者的要求较高。为了更好地使用SAS软件实现剂量反应的Meta分析,由美国哈佛大学开发的应用于剂量反应Meta分析的SAS宏%metadose可以方便地实现剂量反应的Meta分析,并绘制非线性剂量反应曲线,结合实例进行详细介绍。
SAS system is considered as one of international standard software systems in the field of data processing and statistics. However, it requires the user has higher capability due to its complex and difficult programming. For well applying SAS for conducting a meta-analysis, Ruifeng Li and Donna Spiegelman developed a macro named metadose for realizing the dose response meta-analysis and generating the graph. In this paper, we introduce it with specific data.
剂量反应关系的Meta分析是一类新型的Meta分析方法, 相比标准的二分类及连续性资料Meta分析, 此类研究可同时处理三个及以上组别的数据, 并直接估计暴露因素与疾病的剂量反应关系[1]。但此类研究的统计方法较为复杂, 与标准Meta分析有所不同, 也无法用Meta分析的标准软件Review Manager软件实现。目前国内仅有罗美玲[2]、张天嵩[3]、曾宪涛[4]介绍了剂量反应关系Meta分析在Stata软件中的实现方法, 实际上在2010年由美国哈佛大学的Ruifeng Li和Donna Spiegelman共同开发的基于SAS软件的%metadose宏命令能轻松地完成这一类Meta分析方法。鉴于此, 本文结合实例将应用SAS软件%metadose宏命令实现剂量反应Meta分析的方法引入国内, 以期为此类Meta分析提供方法学指导。
SAS(statistical analysis system)软件于1964年由美国北卡罗莱纳州立大学开始研制, 1976年正式推出, 是目前在国际上最具影响力的统计软件之一, 具有完备的数据访问、数据管理、数据分析和数据呈现功能, 目前SAS的最高版本为9.3版本[5]。SAS软件的使用主要靠输入代码编程驱动, 故应用SAS软件有一定的难度, 而利用SAS软件的宏可以减少在完成一些共同任务时必须输入的文本量, 也可以使程序模块化, 使程序具有易读、便于修改、移植、方便重复使用的优点。
SAS宏是一段编辑好的程序, 用户可以在提交SAS程序或SAS命令行中调用。利用%macro语句开始一个宏, 同时给出这个宏的名字, 如:%macro abc; 用%mend语句结束一个宏, 其后给出宏的名字, 如%mend abc。放一个百分数符号(%)在宏名字的前面可以调用一个宏, 如%abc。被定义在一个%macro语句的宏名字后括号内的宏变量称宏参数, 可以直接给出宏参数的值, 也可在调用这个宏时给出这些参数的值[6]。
metadose宏是由美国哈佛大学Ruifeng Li和Donna Spiegelman教授在2010年共同开发的专门用于剂量反应Meta分析的SAS宏, 被免费公布在网上, 网址为:http://www.hsph.harvard.edu/donna-spiegelman/software/metadose/, 打开SAS软件后, 可以将此宏命令粘贴到编辑器中, 以方便后面调用。
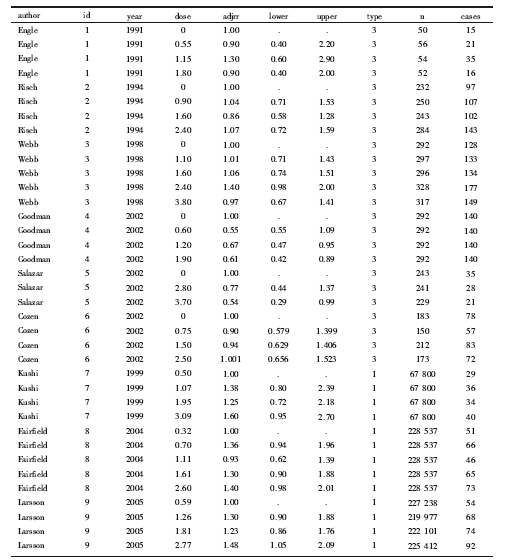
剂量反应的Meta分析只适合于分析三类研究数据:病例对照研究, 以人年为基础的队列研究, 以累计发病数为基础的队列研究。本次研究的具体数据可见曾宪涛《应用STATA做Meta分析》一书[4]。该研究共纳入9篇原始文献, 其中6篇为病例对照研究、3篇为队列研究(为人年队列研究)。数据格式是:研究作者(author, 字符型)、研究编号(id, 数值型)、发表年份(year, 数值型)、剂量(dose, 数值型, 一般取原始暴露剂量区间的中位数)、调整混杂后的效应量(adjrr, 数值型)、效应量95%可信区间(confidence interval, CI)下限(lower, 数值型)、效应量95%CI上限(upper, 数值型)、研究类型(type, 数值型, 分别用1、2、3表示人年队列研究、累计发病数队列研究和病例对照研究)、总数(n, 数值型, 人年队列研究则为各暴露剂量区间的随访人年数, 累计发病数队列研究和病例对照研究则为各暴露剂量区间人口数)、病例(cases, 数值型, 各暴露剂量区间的病例数), 具体数据见表 1。
| 表1 剂量反应关系Meta分析实例数据 |
由于SAS中的各个过程只能对SAS数据集中的数据进行处理, 所以如何将数据转换成SAS数据集是SAS进行统计分析的基础。在数据录入过程中, 每项研究的效应量(adjrr)只允许参照组为1, 相应的95%CI上下限用英文状况下的点表示, 如果遇到同一研究组的其它组adjrr也为1的情况, 那么可以相应地多取几位小数点, 如实例数据Cozen 研究中adjrr=1.001的情况。将示例数据录入SAS软件, 建立allstudies数据集:
data allstudies;
input
author 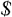
datalines;
Engle 1 1991 0 1 . . 3 50 15
Engle 1 1991 0.55 0.9 0.4 2.2 3 56 21
Engle 1 1991 1.15 1.3 0.6 2.9 3 54 35
Engle 1 1991 1.8 0.9 0.4 2 3 52 16
Risch 2 1994 0 1 . . 3 232 97
Risch 2 1994 0.9 1.04 0.71 1.53 3 250 107
Risch 2 1994 1.6 0.86 0.58 1.28 3 243 102
Risch 2 1994 2.4 1.07 0.72 1.59 3 284 143
……
;
run;
在SAS软件中, 剂量反应的所有分析过程都被整合在metadose宏中, 使用者只需对作者自己设定的参数进行赋值, 就可以很方便地定制各种所需结果, 这里对metadose宏主要的参数进行介绍。
metadose(dat, ratio, UB, LB, Ncase, Ntotal, dose, studyname=citation, studytype, meta=T/N, wt, unit_wt, var_covar, linearCheck=1/0, nk, ci, graphtitle)
其中dat可指定之前所定义的数据集名称, ratio指定效应量变量[因为剂量反应Meta分析只适合于病例对照和队列研究, 故只能用于比值比(odds ratio, OR)和相对危险度(relative risk, RR)二类], UB指定效应量的上限, LB指定效应量的下限(每次分析中可只指定UB或LB), Ncase指定病例数变量, Ntotal指定各区间总数变量, dose指定各组平均暴露剂量变量, studyname指定研究作者变量, studytype指定原始研究类型变量, meta=T/N逻辑选择是否进行多个研究的Meta分析效应量合并, wt指定Meta分析合并效应量所表示的暴露剂量大小, unit_wt表示暴露剂量单位, var_covar指定用于单个研究中协方差矩阵估计的方法, 提供了4种选择G(Greenland method)/H(Hamling method)/GH(both Greenland and Hamling method)/K(用户自定义), 其中系统默认的是GH; linearCheck=0/1指定是否对剂量反应曲线进行非线性检验, nk表示使用限制性立方样条进行非线性剂量反应分析时指定的样条的数目, ci=0/1/2指定合并剂量反应95%CI上下限曲线的绘制方法(0为不绘制95%CI上下限曲线, 1为阴影形式, 2为点线形式), graphtitle表示剂量反应曲线的名称。
将9篇(6篇为病例对照研究, 3篇为队列研究)关于牛奶制品摄入量与卵巢癌发病风险的研究数据录入SAS软件数据集后, 先将下载好的%metadose宏读入SAS软件, 运行一下, 再根据5.1介绍内容对%metadose宏参数进行如下指定:
%metadose(dat = allstudies, ratio = adjrr, UB = upper, Ncase= cases, Ntotal= n, dose = dose, studyname = author, studytype = type, meta = T, wt =1, unit_wt = servings/day, var_covar= GH, linearCheck = 1, ci = 2, graphtitle = milk products and ovarian cancer risk)
从SAS软件自动返回的结果(表2)中可以发现, 9项研究合并的异质性在Greenland和Hamling两种协方差矩阵估计方法下分别是:QG=18.29, P=0.02, QH=19.07, P=0.01, 两个结果相差不大, 表明研究之间还是存在一定的异质性。保守估计的话可以看随机效应模型的结果:ORG及95%CI 1.01(0.94~1.09), P=0.75; ORH及95%CI 1.01(0.94~1.09), P=0.78。提示牛奶制品的摄入量与卵巢癌患病风险间的联系无统计学意义。
| 表2 9项牛奶制品摄入量与卵巢癌发病风险剂量反应分析结果 |
本次研究纳入队列研究和病例对照两种类型的研究, 而合并分析的结果显示具有异质性, 因此我们不妨做一个关于研究类型的亚组分析, 对6篇为病例对照研究和3篇为队列研究按照总体剂量反应Meta分析的方法分开来分析一下, 看是否能找到异质性的来源。6项牛奶制品摄入量与卵巢癌发病风险病例对照研究剂量反应分析结果见表3。Greenland和Hamling两种协方差矩阵估计方法下分别是:QG=7.94, P=0.16, QH=8.95, P=0.11。表明6项病例对照研究结果是同质的。固定效应模型的结果为:ORG及95%CI 0.96(0.91~1.02), P=0.21; ORH及95%CI 0.96(0.91~1.02), P=0.23, 提示牛奶制品的摄入量与卵巢癌患病风险间的联系无统计学意义。
| 表3 6项牛奶制品摄入量与卵巢癌发病风险病例对照研究剂量反应分析结果 |
另外3项牛奶制品摄入量与卵巢癌发病风险的队列对照研究剂量反应分析结果显示(表4), Greenland和Hamling两种协方差矩阵估计方法下分别是:QG=0.09, P=0.96, QH=0.10, P=0.95, 表明3项队列研究结果是同质的。固定效应模型的结果为:ORG及95%CI 1.13(1.04~1.22), P=0.00; ORH及95%CI 1.13(1.05~1.22), P=0.00。提示牛奶制品的摄入量与卵巢癌患病风险间的关系有统计学意义, 则可进一步确定剂量反应的曲线图形, 再观察SAS软件返回的非线性检验的结果:对根据Greenland和Hamling两种方法非线性检验, P值均小于0.05, 表明3项队列研究中牛奶制品摄入量与卵巢癌发病存在非线性剂量反应关系。
| 表4 3项牛奶制品摄入量与卵巢癌发病风险队列研究剂量反应分析结果 |
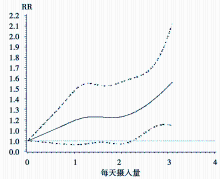
非线性剂量反应Meta分析使用限制性三次样条(restricted cubic spline)来作为链接函数:formula=logrr~rcs(dose, knots)。回归样条(regression spline)本质上是一个分段多项式, 但它一般要求在每个分段点上连续并且二阶可导。即:设自变量数据的范围在区间[a, b], 并根据需要分成k个段 a=t0< t1< …< tk-1< tk=b, 在每个区间[tk-1, ti)分别用一个多项Si(x)式表示, 则回归样条f(x)= Si(x)当x∈ [tk-1, ti), 并且fn(x)在[a, b]存在连续。限制性三次样条是在回归样条的基础上附加要求:样条函数在自变量数据范围两端的两个区间[t0, t1)和(tk-1, tk]内是线性函数, 满足上述性质的样条函数通常用Rcs(x)表示[7], 在SAS软件中%metadose宏将自动对每个研究进行默认nk=4的样条回归, 并以图形方式显示非线性剂量反应曲线。本例中3项牛奶制品摄入量与卵巢癌发病风险队列研究剂量反应曲线如图1。
在流行病学研究中, 如果随着某暴露因素剂量的变化, 研究疾病的频率或联系强度亦相应变化, 则认为这两者存在剂量反应关系。暴露与结局存在剂量反应关系是疾病因果推断的标准之一[8]。剂量反应的Meta分析, 是对多个原始剂量反应研究进行综合汇总, 得出一条合并的剂量反应关系曲线的一类Meta分析, 高质量的剂量反应Meta分析对探讨疾病因果具有非常重要的意义。近年来此类Meta分析文章在国外期刊上发表数量越来越多[1, 8, 9, 10, 11, 12, 13, 14, 15, 16], 而在检索国内万方、CNKI、维普三大数据库后发现:此类Meta分析在国内期刊发表数量凤毛麟角。究其原因:一方面是因为此类Meta分析的统计方法计算较为繁琐, 可以实现的软件操作都涉及到编程, 详细介绍此类Meta分析方法学的文献极少; 另一方面, 高质量的剂量反应Meta分析研究价值较大, 国内作者完成此类Meta分析后, 多选择在国外期刊上发表。实际上此类Meta分析方法学研究还是比较成熟的, 文章的数据也越来越多。只要把国外的研究方法介绍到国内, 完全可以让国内更多的研究者掌握并熟练使用这一类Meta分析方法, 提供更多的循证医学证据。
剂量反应Meta分析的研究思路如下:确定研究的目标后, 一般先收集暴露与疾病的病例对照和队列研究, 在每个病例对照和队列研究中挑选出最高剂量组相对于最低剂量组的RR/OR值的95%CI进行Meta分析合并, 得到一个汇总的RR/OR合并值, 如果这个合并RR/OR值是有统计学意义的, 说明暴露与疾病之类是有关联的, 再进一步进行剂量反应Meta分析探讨这种关联是否存在一种剂量反应关系[10], 标准Meta分析在SAS软件中同样也可以通过宏来实现, 相关的操作方法可参考国内鄢金柱、曾宪涛等的文献[6]。
剂量反应Meta分析收集的数据一般至少要求3个组别以上, 以每个研究最低剂量组为参照组, 该研究其它剂量组均和参照组进行对比。提取各剂量组的平均剂量或中位数剂量做为剂量组的点估计值也就是实例数据中的dose, 如果最低剂量组是开区间则假定最低值为0, 如果最高剂量组是开区间则假定最高剂量组的中点值是最高剂量低值边界的1.5倍[14]。
剂量反应Meta分析从本质上来说是一种回归分析, 因此也具有回归分析的一些特点:剂量反应Meta分析曲线中剂量的取值范围要求在原始研究剂量的最大值和最小值之间, 不能外推至拟合剂量范围之外。在做剂量反应Meta分析中会涉及到一个线性剂量反应关系和非线性剂量反应关系的问题, 一般的做法是先用限制性三次样条(restricted cubic spline)作为链接函数拟合一个非线性模型, 若设定模型自变量包括四个回归样条, 利用卡方检验对第二个和第三个回归样条回归系数作是否同时为0的假设检验, 如果P> 0.05, 则为线性剂量反应关系, 反之则认为存在非线性剂量反应关系[2, 3]。
目前进行剂量反应Meta分析的软件主要有SAS、STATA和R软件, STATA软件利用GLST程序包实现[2, 3, 4], R软件主要通过dosresMeta程序包实现[1]。STATA软件 GLST程序包在2005年由瑞典统计学家Nicola Orsin团队开发, 并迅速得到广大Meta分析爱好者的青睐, 2010年美国哈佛大学的Ruifeng Li和Donna Spiegelman共同开发基于SAS软件的metadose宏命令, Orsini等曾专门撰文进行对比, 显示具有一致的分析结果[17]。本次研究利用相同的数据与曾宪涛书中用STATA软件分析结果也一致[4], R软件dosresMeta程序包则是2013年由Orsini教授的博士研究生Alessio Crippa研发, 目前正在进一步完善中。对比STATA软件和R软件的程序包, SAS软件metadose宏做剂量反仅的优势在于:只需要较少的代码, 就能得到剂反所有的分析结果, 特别是绘图方面, 均由宏程序自己生成。当然这套宏程序也有自身的局限性:灵活性不够, 绘图不够美观。笔者建议剂量反应Meta分析爱好者自学这三种程序后, 配合使用, 用SAS软件metadose宏进行探索性分析, 再由STATA和R软件精细化分析结果和图表。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|