引用本文
陈新林, 文艺, 胡月, 江梅, 武哲丽, 李先涛, 周倩仪, 徐谦, 莫传伟. 生存分析资料进行Meta分析时所需主要结局指标的换算方法. 循证医学, 2016,16(4): 244-246.
CHEN Xin-lin, WEN Yi, HU Yue, JIANG Mei, WU Zhe-li, LI Xian-tao, ZHOU Qian-yi, XU Qian, MO Chuan-wei. The Transformation of the Main Indices for the Meta-analysis of Survival Data. Journal of Evidence-Based Medicine,2016,16(4): 244-246.  
DOI:10.12019/j.issn.1671-5144.2016.04.016
Permissions
Copyright©2016, 《循证医学》编辑部
《循证医学》杂志 版权所有
生存分析资料进行Meta分析时所需主要结局指标的换算方法
陈新林1, 文艺2, 胡月1, 江梅3, 武哲丽1, 李先涛1, 周倩仪3, 徐谦1, 莫传伟1
1. 广州中医药大学基础医学院, 广州 510006
2. 广州中医药大学第一临床学院, 广州 510405
3. 广州医科大学第一附属医院, 广州 510120
莫传伟,Tel：020-36585451, E-mail:mcwgz@gzucm.edu.cn

作者简介: 陈新林（1981-）,男,广东梅州人,副教授,以医学统计和流行病学为主要研究方向。

收稿日期: 2016-01-25
基金项目:基金项目: 国家自然科学基金资助项目（81403296）; 广东省高等学校优秀青年教师资助项目（YQ2015041）; 广州中医药大学“青年英才”资助项目（QNYC20140101）; 广州中医药大学“薪火计划”资助项目（XH20140105）
摘要

生存资料的Meta分析越来越多,但是大部分原始文献并没有全面报告实际死亡数（O）、理论死亡数（E）、风险比（HR）及其方差（V）,本文总结了O-E、HR和V等指标的多种转换公式。希望研究者能够灵活应用这些公式计算生存资料Meta分析的必备指标,并采用HR进行生存资料的Meta分析。

关键词: 生存数据; Meta分析; 实际死亡数; 理论死亡数; 风险比
中图分类号:R195.1 文献标志码:A
The Transformation of the Main Indices for the Meta-analysis of Survival Data
CHEN Xin-lin1, WEN Yi2, HU Yue1, JIANG Mei3, WU Zhe-li1, LI Xian-tao1, ZHOU Qian-yi3, XU Qian1, MO Chuan-wei1
1. Basic Medical College, Guangzhou University of Chinese Medicine, Guangzhou 510006, China
2. The First Clinical Medical School, Guangzhou University of Chinese Medicine, Guangzhou 510405, China
3. The First Affiliated Hospital, Guangzhou Medical University, Guangzhou 510120, China
Abstract

Meta-analysis of survival data is becoming more and more. However, most of the original literature did not offer the comprehensive porting： logrank observed events （O）, logrank expected events （E）, hazard ratio （HR） and logrank variance （V）. This paper summarized a variety of methods about how to transform O-E, HR and V. We hope that the researcher can use the methods freely, and use HR in the meta-analysis of survival data.

Key words: survival data; meta-analysis; logrank observed events; logrank expected events; hazard ratio

生存分析（survival analysis）是将终点事件（结局）的出现与否和达到终点所经历的时间结合起来当作预后的一类统计分析方法。生存分析一方面考虑患者的生存结局（生存、死亡或删失）, 另外一方面考虑患者的生存时间（survival time）。多因素生存分析经常采用Cox模型, 其表达式为：

h(t)=h0(t) exp (β 1X1+β 2X2+…+β pXp)

[h(t)]为具有协变量[X1]、[X2]、…、[Xp]的个体在[t]时刻的风险函数; [h0(t)]是基准风险函数; [β 1]、[β 2]、…、[β p]为各协变量的系数, 通过变换可以算得[HRj=exp(β j)]。HR也称为风险比（hazard ratio）, 表示两个个体风险函数之比。由此可见, 生存分析的Meta分析应该采用HR来分析, 运用相对危险度（relative risk, RR）或者比值比（odds ratio, OR）进行分析都是不恰当的, 容易导致错误的结果[1, 2]。

1 生存资料的Meta分析

生存资料的Meta分析越来越多, 生存资料的合并lnHR可以通过以下公式计算：

[∑ (O-E)/∑ (1/V* ), 或=[∑ (lnHR/V* )/∑ (1/V* )]。其中O、E（logrank observed events, expected events）分别表示干预组的实际死亡数和理论死亡数, lnHR表示HR的自然对数值; [V* =1/V], 表示lnHR的方差值[2, 3, 4]。因此计算合并lnHR, 需要知道每个文献的O、E、V或者lnHR（或HR）、V。O-E、HR和V是生存资料Meta分析的主要指标, 三者之间存在以下关系：

[HR=exp(O-E)/V] 公式（1）

部分文献给出生存曲线图, 如何从生存曲线图中算出O、E、V和HR等数据, 可参考相关文献[4, 5]。大部分原始文献一般不会直接报告O-E和V（或HR和V）, 或者只报告部分指标。同时, 这些文献又报告了其它指标, 比如HR的95%置信区间（confidence interval, CI）或者HR的P值等。这里将文献主要分为两类：（1）只报告O-E或HR; （2）没有报告O-E、HR和V。

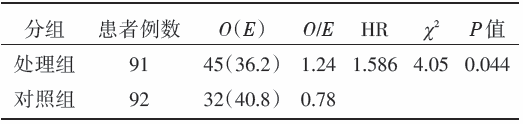
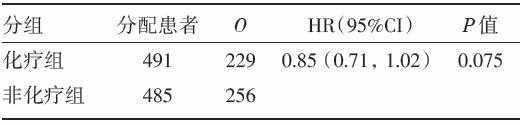
我们结合下面两个例子, 介绍如何根据文献报告的其它指标求解O-E、HR和V。例1：医学研究理事会开展一项晚期宫颈癌的随机对照试验, 比较单纯放疗（对照组）、放疗+放射增敏剂（处理组）的疗效[6], 纳入183例患者, 处理组91例, 对照组92例, 资料见表1。例2：医学研究理事会开展膀胱癌的随机对照试验, 比较化疗组和非化疗组的疗效, 得到表2的资料[7]。

表1 晚期宫颈癌的资料[6]
表2 膀胱癌的资料[7]
2 只报告O-E或HR

部分文献只报告O-E或HR, 没有报告V; 这时需要根据文献报告的其它指标计算V。主要包括以下几种情况：

①报告两组O、E或HR

公式（2）

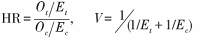
其中[Ot]、[Et]分别为处理组的实际死亡数和理论死亡数; [Oc]、[Ec]分别为对照组的实际死亡数和理论死亡数; 例如表1报告[Ot]、[Et]、[Oc]、[Ec]分别是45、36.2、32和40.8, 根据公式（2）可算出[HR=1.58], [V=1(1/36.2+1/40.8)=19.18], [Ot]-[Et]=8.8。

②报告HR、[Ot]和[Oc]（两组分配比例为1∶ 1）

[V=Ot× Oc/O] 公式（3）

其中[O=Ot+Oc]为两组的实际死亡数之和。例如表1报告HR=1.586, [Ot]、[Oc]、O分别为45、32和77, 根据公式（3）算出V=18.7, 根据公式（1）算出[Ot]-[Et]=8.6。

③报告HR和O（两组分配比例为1∶ 1）

[V≈ O/4] 公式（4）

当两组样本量比例为1∶ 1, 公式（3）可化简为公式（4）。例如表1报告HR=1.586, [O]为77, 根据公式（4）算出[V≈ 77/4=19.25]; 根据公式（1）算出O-E=8.8。

④报告HR、[O]、[Rt]和[Rc]（两组分配比例不是1∶ 1）

[V=O× Rt× Rc/(Rt+Rc)2] 公式（5）

其中[Rt]、[Rc]分别是处理组和对照组随机分配的例数。例如表2报告HR=0.85, O、[Rt]、[Rc]分别为485（229+256）、491、485, 根据公式（5）可算出V=485× 491× 485/（491+485）2=121.25。根据公式（1） 算出O-E=-19.70。

⑤报告HR和其95%CI

公式（6）

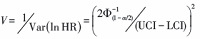
当[α =0.05]时, UCI、LCI分别表示HR 95%CI的上限和下限的自然对数值, [Φ -1(1-0.05/2)=1.96]。例如表2报告HR=0.85, 其95%CI为（0.71, 1.02）, 先求出UCI（ln（1.02））、LCI（ln（0.71））两个数值, 然后根据公式（6）算出V=〔(2× 1.96)/[ln(1.02)-ln(0.71)]〕2=117.07; 最后根据公式（1）得到O-E=-19.03。

虽然①、②、③、④和⑤的公式不一样, 但是其得到的结果是一样的。例如①、②和③都使用同一个例子的资料, 排除舍入误差的影响, 可以认为计算结果基本相同。

3 没有报告O-E、HR和V

部分文献对O-E、HR和V都没有报告。如果文献报告了足够的其它指标, 也可以算出O-E、HR和V。主要包括以下几种情况：

①报告P值、[Ot]和[Oc]（两组分配比例为1∶ 1）

公式（7）

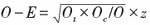
其中z表示（P/2）值对应的标准正态分布函数值, 根据表1求出P/2=0.044/2=0.022, 对应的z=2.014, 得到O-E=8.7。根据公式（3）算出V=18.3。

②报告P值和O（两组分配比例为1∶ 1）

[O-E=1/2× O× z] 公式（8）

根据表1知道P/2=0.044/2=0.022, 对应的z=2.014; O为77（45+32）, 得到O-E=8.8。根据公式（4）算出V=19.25。

③报告P值、[O]、[Rt]和[Rc]（两组分配比例不是1∶ 1）

[O-E=O× Rt× Rc/(Rt+Rc)× z] 公式（9）

[Rt]、[Rc]分别是处理组和对照组随机分配的例数。例如表2报告P=0.075, z=1.78; O、[Rt]、[Rc]分别为485（229+256）、491、485; 根据公式（9）得到O-E=19.60。根据公式（5）计算V=117.07。

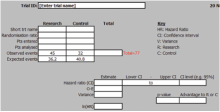
Tierney等[4]将上述程序编制成Excel计算程序, 大家可以上网下载。网址为http：//www.biomedcentral.com/content/supplementary/1745-6215-8-16-S1.xls。例如表1报告[Ot]、[Et]、[Oc]、[Ec]分别是45、36.2、32和40.8。下载并打开这个Excel, 在“ （1）_Summary_Data” 工作表中录入这四个数（见图1）。然后点击“ （4）_Output_Information” 工作表（见图2）, 可以得到以下结果：HR=1.58、HR 95%CI为（1.01, 2.48）、V=19.18和O-E=8.83。获得O-E、HR（lnHR）和V之后, 可以根据公式或者采用RevMan软件、STATA、R等软件计算出合并lnHR。

图1 录入数据

图2 O-E、HR 和V等指标的结果

4 小 结

生存资料的Meta分析越来越普遍, 但是如何基于不同已发表文献提供的信息换算出O-E、HR和V等指标将直接决定后续的分析结果能否建立在尽可能多的研究报告上, 例如Lampropoulos等[8]研究转化生长因子β （TGF-β ）对肠癌患者生存时间的预后作用, 该作者报告TGF-β 对生存时间预后的HR为4.675 3, 其置信区间为（2.085 2, 10.482 7）, 根据公式（6）或者使用图1, 计算得出V=5.89、O-E=9.09。本文章结合Parmar[2]、Tierney[4]等文献, 总结了O-E、HR和V等指标的多种转换公式。希望研究者能够灵活应用这些公式计算生存资料Meta分析的指标, 并采用风险比HR进行生存资料的Meta分析。

The authors have declared that no competing interests exist.

参考文献
[1] 王权, 何曦冉, 蒋林, 等. 风险比在生存资料Meta分析中的应用[J]. 中国循证心血管医学杂志, 2013, 5(6): 559-560. [本文引用:1]
[2] Parmar MK, Torri V, Stewart L. Extracting summary statistics to perform meta-analyses of the published literature for survival endpoints[J]. Stat Med, 1998, 17(24): 2815-2834. [本文引用:3]
[3] Yusuf S, Peto R, Lewis J, et al. Beta blockade during and after myocardial infarction: An overview of the rand omized trials[J]. Prog Cardiovasc Dis, 1985, 27(5): 335-371. [本文引用:1]
[4] Tierney JF, Stewart LA, Ghersi D, et al. Practical methods for incorporating summary time-to-event data into meta-analysis[J]. Trials, 2007, 8: 16. [本文引用:4]
[5] 周支瑞, 张天嵩, 李博, 等. 生存曲线中Meta分析适宜数据的提取与转换[J]. 中国循证心血管医学杂志, 2014, 6(3): 243-247. [本文引用:1]
[6] Medical Research Council Working Party. A trial of Ro 03-8799 (Pimonidazole) in carcinoma of the uterine cervix: An interim report from the medical research council working party on advanced carcinoma of the cervix[J]. Radiother Oncol, 1993, 26(2): 93-103. [本文引用:1]
[7] International collaboration of trialists on behalf of the medical research council Advanced bladder cancer working party. Neoadjuvant Cisplatin, Methotrexate, and Vinblastine chemotherapy for muscle-invasive bladder cancer: A rand omised controlled trial. International collaboration of trialists[J]. Lancet, 1999, 354(9178): 533-540. [本文引用:1]
[8] Lampropoulos P, Zizi-Sermpetzoglou A, Rizos S, et al. Prognostic significance of transforming growth factor beta (TGF-beta) signaling axis molecules and E-cadherin in colorectal cancer[J]. Tumour Biol, 2012, 33(4): 1005-1014. [本文引用:1]