诊断性研究常常以信息丰富的ROC曲线来表示诊断效能情况, 诊断界值的选取并不会改变ROC曲线对该种疾病的诊断性能的评价^[4]。通过选取合适的cut-off值, 诊断的效能就反应在此时cut-off值对应的各种诊断指标, 如真阳性（true positive, TP）、假阳性（false positive, FP）、假阴性（false negative, FN）和真阴性（true negative, TN）中, 常用于诊断性分析的四格表如表1所示。

表1

表1

表1 受试诊断研究数据报告四格表

表1 受试诊断研究数据报告四格表

在诊断性Meta分析实践中, 研究结果最直接的信息呈现方式为TP、FP、FN和TN, 当给出了TP、FP、FN和TN等对应的诊断数据后, 通过表2所给的公式, 分别计算出各种诊断性能评价的指标如敏感性、特异性、阳性预测值以及阴性预测值, 这是文章中常见的数据给出形式。此外, 还有一些数据形式要通过简单计算才能得出, 如患者人数和健康人数, 一些数据给出情况如表2所示。

表2

表2

表2 常见的与诊断性研究相关的指标和公式

表2 常见的与诊断性研究相关的指标和公式

在做诊断性Meta分析时, 我们优先想得到与诊断直接相关参数, 或者用表2中的公式通过简单计算转换即可得到的数据。但在有些情况下, 在我们所纳入的文献中并未提供以上完整的数据, 如一种在文章中较常见的数据给出形式为仅提供Sen、Spe以及N值, 缺少能完整计算出TP、FP、FN和TN的一个或两个参数, 甚至有时作者会对其研究中非重点的诊断数据干脆仅以ROC曲线的图表展示^[5], 在这种情况下, 尽可能地得到或者转换为有用信息的方法非常重要。

解决这种问题的一个思路就是求解上述方程组, 由于在诊断性研究中, TP、FP、FN和TN值代表的是各种研究结果的例数, 均为正整数, 因此通过文章中提供的不完整信息组成的方程组, 通过求其正整数解, 进一步得出TP、FP、FN和TN值也就成为可能。据此, 我们总结了常见的几种数据提取的情形和方法（如表3所示）。

表3

表3

表3 几种数据的给出形式和计算求解方法

表3 几种数据的给出形式和计算求解方法

Excel具有十分强大的功能, 其宏命令在许多研究中应用广泛^{[6, 7]}, 本文根据表3对应的公式和原则, 通过Excel 2013平台来说明在缺少部分数据的情况下, 有关TP、FP、FN和TN值的计算。

3.1 Excel中诊断性研究数据的引用和处理

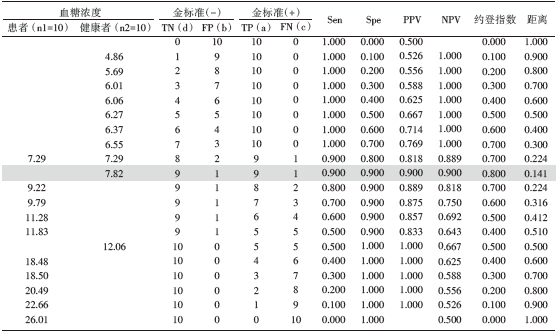
为了方便理解和操作, 以Lasko等^[2]文章中的数据为例来说明, 例子中有10名糖尿病患者和10名健康人（共20人）接受口服葡萄糖耐量试验^[2], 已分别计算出TN、FP、TP、FN值, 我们利用文章中给出的血糖浓度值, 在Excel中很容易计算出Sen、Spe、PPV、NPV、约登指数和到点（0, 1）距离等数据（如表4所示）。

表4

表4

表4 接受口服葡萄糖耐量试验的实例数据

表4 接受口服葡萄糖耐量试验的实例数据

3.2 Excel绘制ROC曲线的解读

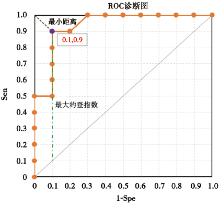
通过Excel绘制出的ROC曲线图可知, 在最大约登指数和最小距离点处所取的Sen和Spe分别为0.90和0.90, PPV和NPV分别为0.90和0.90, 这些均与文章中报道的相一致（如图1所示）。

图1

	Figure Option ViewDownloadNew Window
	图1 口服葡萄糖耐量试验数据确定的ROC 曲线

3.3 Excel宏文件提取不完整数据

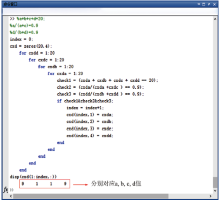
根据上述运算思路, 以制作的Excel宏程序进行运算, 为方便理解, 在此以常见的一种数据给出形式（3）中的公式三为例（如表3）。已知Sen=0.9、Spe=0.9和N=20, 根据上述求解正整数思路和算法, 可以很方便求出对应的值：TP=9、FP=1、FN=1和TN=9, 利用这种思路计算的结果与原文一致（如图2所示）。

图2

	Figure Option ViewDownloadNew Window
	图2 EXCEL 宏文件进行数据计算

3.4 提取数据的验证

为了进一步验证计算的准确性, 在此采用一种数学矩阵计算软件MATLAB进行验证（如图3所示）, 运算出的结果与Excel宏计算出来的结果一致, 接下来我们对其他数据给出形式也进行了验算, 计算结果也与预期一致（数据省略）。

图3

	Figure Option ViewDownloadNew Window
	图3 MATLAB 对计算结果进行验证

Excel作为一种常用于数据计算和整理的软件, 有强大的功能, 被应用于生存曲线中数据的提取^{[8, 9]}和ROC曲线的绘制^[10]。ROC曲线被广泛地应用于生物标志性分子对某种疾病的诊断性分析中, 通过一系列原则, 选择最合适的cut-off值, 确定某分子对某种疾病诊断的敏感性和特异性值, 以及ROC曲线下面积（area under the curve, AUC）的大小^[11]。在先前的研究中, 我们介绍了一种方法, 能很好地从ROC曲线图中提取敏感性和特异性值, 这种方法解决了我们在做Meta分析过程中, 仅给出ROC曲线而无具体数据时导致文章无法纳入的问题^[3]。本文进一步提出几种诊断性Meta分析过程中数据给出不完整时的情形（如表3所示）, 并提供一种不完整数据提取的解决方案。

以Lasko文章中报道的数据为例, 通过Excel软件对数据进行简单的处理, 以绘制的ROC曲线图和计算表格, 清晰地得出最大约登指数和对应的敏感性和特异性值。我们以一种常见的数据给出形式为例, 基于Excel软件, 准确地计算出了TP、FP、FN和TN值。根据所提出的计算思路和方法, 我们在MATLAB软件中进行验证, 结果表明这些思路和方法具有较高的可靠性。

我们在此提供的方案是基于表2中诊断性分析相关的基本公式进行的, 实质是利用计算机软件优势, 对所需提取的TP、FP、FN和TN值, 求方程组的正整数解过程。这种方法虽然很方便, 但是也存在自身的局限性：一方面, 在进行初始值运算时, 可能会遇到找不到整数解的情况, 这时可以尝试调整一下保留小数点的精确度值, 再重新求解就可以了。另一方面, 这种求整数解的过程是在限定的人数范围内, 虽然常规情况下都可得出唯一的解, 但是也有少数情况下可得出多组解, 当遇到这种情况时, 可以结合文章中提供的其他信息得出真正的解。