引用本文
何杰宇, 孙金芳, 王莉娜, 闵捷, 余小金. 基于再抽样模拟表达谱研究Meta分析的假设检验方法.循证医学, 2016,17(3): 175-179
HE Jie-yu, SUN Jin-fang, WANG Li-na, MIN Jie, YU Xiao-jin. Hypothesis Test Based on Re-Sampling for Meta-Analysis of Gene Expression Profiling Studies Application. Journal of Evidence-based Medicine, 2016,17(3): 175-179  
Doi:10.12019/j.issn.1671-5144.2017.03.014
Permissions
Copyright©2017, 《循证医学》编辑部
《循证医学》杂志 版权所有
基于再抽样模拟表达谱研究Meta分析的假设检验方法
何杰宇, 孙金芳, 王莉娜, 闵捷, 余小金
东南大学公共卫生学院, 南京 210009
通讯作者:余小金,Tel：025-83272562;E-mail：101006181@seu.edu.cn

作者简介: 何杰宇（1989-）,男,云南文山人,硕士研究生,研究方向为卫生统计学在医学中的应用。

基金:国家自然科学基金资助项目（81673274）
摘要

目的 介绍基于再抽样模拟表达谱研究Meta分析的假设检验方法及其软件实现。方法 采用经验分布模拟抽样方法实现表达谱研究Meta分析中计数效应指标的假设检验,以甲状腺癌表达谱研究Meta分析为例,说明实现过程,并采用SAS软件编程实现。结果 基于经验分布的再抽样方法可得到某特定重复报道研究数下基因数的分布,从而对分析中得到的计数效应指标进行假设检验。结论 基于再抽样模拟表达谱研究Meta分析的假设检验,可用于无理论分布效应量的假设检验,基因表达谱研究的系统评价与Meta分析为其主要应用领域,可推广到其他类似研究。

关键词: Meta分析; 再抽样模拟; 表达谱研究; 假设检验
中图分类号:R195.1 文献标识码:A 收稿日期:2016-09-27
Hypothesis Test Based on Re-Sampling for Meta-Analysis of Gene Expression Profiling Studies Application
HE Jie-yu, SUN Jin-fang, WANG Li-na, MIN Jie, YU Xiao-jin
School of Public Health, Southeast University, Nanjing 210009, China
Abstract

Objective To introduction the hypothesis test of expression profiling studies meta-analysis based on re-sampling method and the application with SAS.Method A real example of gene expression profiling studies was used to demonstrate the usage and procedure of the hypothesis test of meta-analysis based on re-sampling method.Results Genes were identified in different studies with consistently reported.Conclusion The hypothesis test of expression profiling meta-analysis based on re-sampling method can apply in the effect size with no specific distribution such as the meta-analysis of gene expression profiling studies to identify candidate biomarkers and thus can be applied in other field.

Key words: meta-analysis; re-sampling method; expression profiling studies; hypothesis

Meta分析方法作为综合分析一系列独立研究的强有力工具[1], 在医学领域得到广泛应用。对于均数差、率比等常见效应量的综合, 已经有成熟的统计学方法和相关的软件实现。当研究效应量不是这些常见的指标时, 往往对统计学方法提出挑战。

基因表达研究是寻找风险及预后相关差异性表达基因的最普遍方法, 不同研究常对系列备选基因进行检测, 并报道差异性表达的基因, 包括上调或下调表达的基因。此类研究, 同时比较的基因几千到几万不等, 只有其中小部分基因有统计学意义; 研究间样品预处理、检测平台和分析方法等皆存在差异, 使得相同癌症的同种组织、不同研究报道结果也不尽相同[2]。综合此类研究的最常用的方法是将基因在某类癌症中差异性表达（有统计学意义）的研究数, 或称重复数作为效应指标[3, 4, 5, 6, 7], 以此效应指标进行排序, 效应指标越大（重复研究数越多）, 次基因次序越高, 其可作为生物标志物的可能就越大。该法基于P值划分结果, 因无法考虑样本量等影响P值大小的因素在内而备受诟病, 此方法也未考虑结果的不确定性, 即不能像经典Meta分析一样, 对综合指标进行假设检验。Griffith等[8]提出了对该指标的假设检验方法, 应用于甲状腺癌的差异表达基因的Meta分析并验证其排序基因的有效性。本文将基于实例介绍该法的基本原理及其SAS软件实现。

1 原理和方法
1.1 基因表达数据Meta分析的常用方法

基因表达数据Meta分析方法, 由于涉及来自不同平台的大量的基因表达数据, 因此, 目前采用较多的是借鉴传统唱票法的思路, 首先统计出各个研究报道的差异性表达基因信息如样本量、基因表达差异方向、改变倍数等; 其次, 统计同一基因在不同文章被重复报道的次数（方向相同）; 最后, 以重复报道次数、样本量和平均改变倍数对各个基因进行排序; 次序越高, 此基因差异性表达的可能性就越大。

1.2 唱票法Meta分析效应指标的假设检验原理

Griffith等[8]结合再抽样模拟对一致基因的研究数（即重复研究数）进行假设检验, 其基本原理是：假设各个研究报道差异性表达基因是相互独立的, 以此假设为前提进行基于实际数据的再抽样模拟, 进而得到M个研究中, N（N=2, 3, 4, …N≤ M）个研究报道差异性表达的基因数目的概率分布, 用此分布对实际数据的N个研究报道差异性表达基因数目进行检验, 若P值小于检验水准, 则拒绝原假设, 认为各个研究之间报道的差异性表达基因是相互关联的, 对各个差异性表达基因进行排序, 从而筛选具有潜在生物学价值的基因。

1.3 唱票法Meta分析效应指标的假设检验方法

由于各研究使用的检测平台与基因识别码不尽相同, 分析前需统一各研究报道的差异性表达基因识别码（如：统一转换为Entrz gene id）。统计各研究报道的平台检测基因数目, 差异性表达基因数、名称、方向以及检测样本量; 以重复研究数、检测样本对各差异性表达基因进行排序并对其进行假设检验。

检验方法如下：

假设Meta分析综合的研究总数为M, Si（i=1, 2, 3, …M）表示第i个研究所检测的基因数, Ui（i=1, 2, 3, …M）表示第i个研究报道的差异上调表达基因数, Di（i=1, 2, 3, …M）表示第i个研究报道的差异下调表达基因数目（Si、Ui和Di均为第i个真实研究所报道基因转换为统一基因编码后的数值）。

根据实际数据, 统计M个研究中, 各研究所报道的检测基因数（Si）, 上调基因数目（Ui）, 下调基因数目（Di）。

① 在大小为Si的抽样池中随机抽取Ui个基因标记为上调, 抽取Di个基因标记为下调, i=1, 2, 3…M;

② 以相同方法分别对余下的M-1个研究进行抽样, 得到模拟数据集;

③ 在模拟数据集中, 清点1~M个模拟研究结果一致性上调或下调的基因数, 例如：J=2, 表示基因在2个研究者中一致性上调, CJ=#（J=i）, i=2, 3, …M表示在i（i=2, 3, …M）共同上调或下调的基因数;

④ 重复①~③过程K（如K=10 000）次;

⑤ 得到CJ（J=2, 3, 4, …, J≤ M）的经验概率分布。

统计真实数据中各个差异性表达基因在不同研究中的重复报道数, 结合模拟得到CJ（J=2, 3, …M）的经验概率分布, 即可对各重复研究数下差异性表达基因数目进行假设检验, 能考虑结果综合的不确定性, 得到更为合理的结果。

2 实例分析

数据来源于Griffith等[8]的Meta分析文献, 文献探究甲状腺癌表达谱中潜在的生物标志物, 甲状腺癌组织与癌旁组织或腺瘤比较的5篇研究（单一平台）, 数据见表1（Affymetrix HG-U95A注释文件下载地址：http：//www.affymetrix.com/estore/, 基因ID转换工具：https：//david.ncifcrf.gov/）。

进行再抽样模拟, 以表1中Barden研究为例：

① 在基因抽样池S4（12 376）中随机抽取U4（49）个基因, 标记为上调基因, 抽取D4（40）个基因, 标记为下调基因;

② 对其他4个研究也进行与①相同操作, 得到模拟数据;

③ 清点各个基因被抽到次数（方向相同）, 对被抽到次数为2、3、4、5的基因数进行统计并计为C2、C3、C4、C5;

④ 重复①~③过程10 000次;

⑤ 统计模拟数据, 得到C2、C3、C4、C5的经验概率分布（SAS程序见附录）。

运用传统唱票法对5篇纳入文献的差异性表达基因进行排序, 并结合C2、C3, C4、C5的经验概率分布进行假设检验。

表1 纳入甲状腺癌组织与癌旁组织或腺瘤比较研究的数据
3 结果及分析

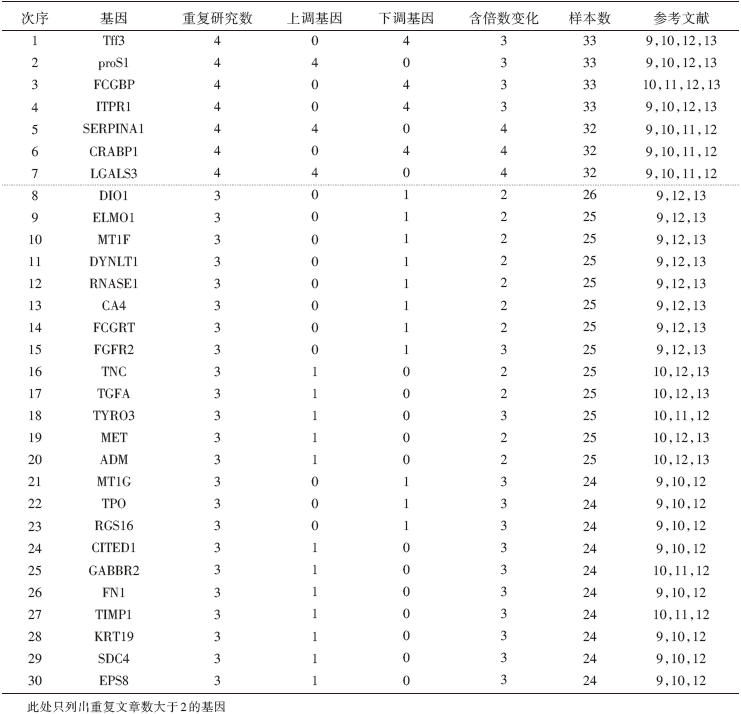
用唱票法对5篇研究所报道的差异性表达基因进行排序（见表2）, 7个基因在4篇研究中重复报道差异性表达, 其中3个为上调表达, 4个为下调表达; 23个基因在3篇研究中被报道差异性表达, 上调表达基因数为12, 下调表达基因数为11; 50个基因在2篇研究中被报道差异性表达, 24个基因上调表达, 26个基因下调表达。

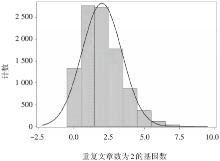
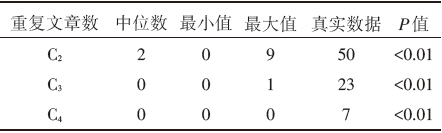
经过再抽样模拟, 5篇研究中, 2篇研究报道相同方向差异性表达基因的中位数为2, 最小值和最大值分别为0和9, 真实数据为50, 经验分布直方图显示, 完全随机条件下, 5篇研究报道任2篇研究报道差异性表达基因数大于等于50的概率小于0.01（见表3和图1）; 重复研究数为3和4的基因数, 模拟数据都为0, 对应的真实数据分别为23和7, P值均小于0.01。

表2 差异性表达基因唱票法排序的结果
表3 差异性表达基因再抽样模拟的结果

图1 C2的经验概率分布图

4 讨 论

基因表达谱研究, 样本量少维度高, 其识别出的差异性表达基因很有可能是假阳性或者假阴性结果, 不同研究对相同问题的结果往往差异巨大, 因此, 该类研究的Meta分析对统计学方法提出了实际的挑战。

对各个研究中差异性表达基因重复次数进行计数, 并以一定规则排序, 差异性表达基因排序越高, 表明其生物学价值越大, 其本质是基于P值的传统唱票法Meta分析, 虽然将样本量作为第二排序标准, 在一定程度上考虑了样本量的影响, 但是未对效应指标进行假设检验, 因而传统唱票法Meta分析在学术界被认为有缺陷[14, 15]。

本文介绍该类研究Meta分析的假设检验方法[8], 在传统唱票法的基础上, 结合实际数据进行再抽样模拟, 对差异性表达基因排序的同时给出相应的假设检验结果, 弥补了该类Meta分析不能进行假设检验的缺陷, 能提供更为可靠的信息。Rikke等[16]用45名肺癌患者癌组织及癌旁组织对Peng等[6]基于唱票法识别出的肺癌microRNA潜在标志物结果进行外部验证, 发现该方法可作为生物标志物识别方法; Griffith等[8]亦在直肠癌表达谱研究Meta分析中验证此方法排序结果的有效性, 在重复研究数在5以上的38个基因中, 在基因或蛋白水平被验证有生物学效应的基因有32个, 占84.26%, 因此, 从目前的研究结果来看, 该类方法有着重要的应用前景。

本文介绍的模拟方法是基于样本经验分布的再抽样模拟。值得一提的是, 经验概率分布的构造是相对灵活的, 本文设定χ 2是重复研究数恰好为2时, 差异性表达基因数目的经验概率分布, 实际数据的计数亦是如此设定。进行相应假设检验时, 无效经验概率分布的构造应与实际数据的计数方法一致。

该法在实际应用中的局限性可以从三个方面考虑：首先, 在实际数据的提取中, 检测平台与Entrz id匹配成功率常常不能达到100%, 在不同平台结果合成时难免损失部分信息; 第二, 模拟结果对各个研究模拟抽样池（能匹配至Entrz id的基因数）敏感, 部分研究因无法获得其检测平台注释文件而无法进行匹配, 只能估计匹配成功率乘以平台报道基因检测数作为模拟抽样池, 因而不能完全反映真实情况; 第三, 不同研究对差异性表达基因定义标准不一, 有的研究以基因表达变化倍数排序, 只报道部分差异性表达基因, 造成信息缺失, 并为综合此类研究带来不确定性。在实际应用中, 可以相对保守地选取排序靠前的基因进行进一步分析, 如本文示例中, 虽然重复研究数为2的50个差异性表达基因假设检验结果显示有统计学意义, 为降低可能存在的假阳性, 可选取重复研究数为3的23个基因或重复性研究数为4的7个基因进行进一步的分析。

总之, 该法在对基因表达差异进行计数的同时, 结合模拟抽样方法进行假设检验。能够充分考虑结果的不确定性, 提供更为全面可靠的信息, 可为此类数据的综合分析提供新的分析思路。

附录：SAS核心程序

%macro mid（num=, maxs=）; /* “ 对模拟数据集进行处理,

num=模拟文章数, maxs=最大抽样池” * /

study_up = j（200, & maxs. , 0）;

study_down = j（200, & maxs. , 0）;

study_final =j（200, & maxs. , 0）;

%do n = 1%to& num. ;

study_up& n. = （h& n. =1）;

study_down& n. = （h& n. =-1）;

study_up=study_up+study_up& n. ;

study_down=study_down+abs（study_down& n. ）;

%end;

%mend mid;

%macro outcir（idd=）; /* 将10000次模拟拆做50次循环, 每

次循环模拟200次 idd=循环次数 * /

%do qq = 1%to& idd. ;

proc iml ;

start stu（size, up, down）; /* 单个研究抽样 size=抽样池,

up=上调基因数目, down=下调基因数目* /

id = （1：size）;

sty1 = j（200, size, 0）;

do i = 1 to 200;

if up = 0 then do;

loci_down = sample（id, down, “ noreplace” ）;

sty1[i, loci_down] = -1;

end;

else do;

if down = 0 then do;

loci_up = sample（id, up, “ noreplace” ）;

sty1[i, loci_up] = 1;

end;

else do;

loci_up = sample（id, up, “ noreplace” ）;

id_down = remove（id, loci_up）;

loci_down = sample（id_down, down, “ noreplace” ）;

sty1[i, loci_up] = 1;

sty1[i, loci_down] = -1;

end;

end;

end;

if size = 12376 then ; return（sty1）;

else;

do;

nblk = 12376 - size;

blk = j（200, nblk, 0）;

return （sty1||blk）;

end;

finish;

/* 对各个研究分别进行抽样* /

h1 = stu(12376, 48, 80);

h2 = stu(12376, 49, 49);

h3 = stu(12376, 49, 40);

h4 = stu(12376, 22, 25);

h5 = stu(12376, 4, 4);

%mid(num=5, maxs=12376);

/* 计数* /

study_dir =j(200, 12376, 0);

study_null=j(200, 12376, 0);

do cc = 1 to 12376;

do rr = 1 to 200;

if study_down[rr, cc]=0 then study_dir[rr, cc]=study_up[rr, cc];

else do;

if study_up[rr, cc]=0 then study_dir[rr, cc]=study_down[rr, cc];

else study_dir[rr, cc]=study_null[rr, cc];

end;

end;

end;

a =(study_dir=2);

b =(study_dir=3);

c =(study_dir=4);

d =(study_dir=5);

count2_& qq. =a[, +];

count3_& qq. =b[, +];

count4_& qq. =c[, +];

count5_& qq. =d[, +];

aaa = count2_& qq. ||count3_& qq. ||count4_& qq. ||count5

_& qq. ;

create test& qq. from aaa;

append from aaa;

close test& qq. ;

quit;

%end;

%mend outcir;

%outcir(idd=50);

The authors have declared that no competing interests exist.

参考文献
[1] 孙振球. 医学统计学[M]. 3版. 北京: 人民卫生出版社, 2010. [本文引用:1]
[2] 赖铭裕, 聂家艳, 黄杰安, 等. 结肠癌与正常结肠组织基因表达谱的差异性研究[J]. 实用医学杂志, 2009, 25(21): 3557-3559. [本文引用:1]
[3] LV M, ZHU X, CHEN W, et al. Searching for cand idate microRNA biomarkers in detection of breast cancer: A meta-analysis[J]. Cancer Biomark, 2013, 13(5): 395-401. [本文引用:1]
[4] LI M Y, HU X X. Meta-analysis of microRNA expression profiling studies in human cervical cancer[J]. Med Oncol, 2015, 32(6): 510. [本文引用:1]
[5] CHAN S K, GRIFFITH O L, TAI I T, et al. Meta-analysis of colorectal cancer gene expression profiling studies identifies consistently reported cand idate biomarkers[J]. Cancer Epidemiol Biomarkers Prev, 2008, 17(17): 543-552. [本文引用:1]
[6] PENG G, YIN Z, LI X, et al. Meta-analysis of human lung cancer microRNA expression profiling studies comparing cancer tissues with normal tissues[J]. J Exp Clin Cancer Res, 2012, 31(1): 1-8. [本文引用:2]
[7] MILLER B G, STAMATOYANNOPOULOS J A. Integrative meta-analysis of differential gene expression in acute myeloid leukemia[J]. PLoS One, 2010, 5(3): e9466. [本文引用:1]
[8] GRIFFITH O L, MELCK A, JONES S J, et al. Meta-analysis and meta-review of thyroid cancer gene expression profiling studies identifies important diagnostic biomarkers[J]. J Clin Oncol, 2006, 24(31): 5043-5051. [本文引用:5]
[9] HUANG Y, PRASAD M, LEMON W J, et al. Gene expression in papillary thyroid carcinoma reveals highly consistent profiles[J]. Proc Natl Acad Sci U S A. , 2001, 98(26): 15044-15049. [本文引用:1]
[10] FINLEY D J, ARORA N, ZHU B, et al. Molecular profiling distinguishes papillary carcinoma from benign thyroid nodules[J]. J Clin Endocrinol Metab, 2004, 89(7): 3214-3223. [本文引用:1]
[11] HAWTHORN L, STEIN L, VARMA R, et al. TIMP1 and SERPIN-A overexpression and TFF3 and CRABP1
underexpression as biomarkers for papillary thyroid carcinoma[J]. Head & neck, 2004, 26(12): 1069-1083. [本文引用:1]
[12] FINLEY D J, ZHU B, BARDEN C B, et al. Discrimination of benign and malignant thyroid nodules by molecular profiling[J]. Ann Surg, 2004, 240(3): 425-436. [本文引用:1]
[13] BARDEN C B, SHISTER K W, ZHU B, et al. Classification of follicular thyroid tumors by molecular signature: results of gene profiling[J]. Clin Cancer Res, 2003, 9(5): 1792-1800. [本文引用:1]
[14] BORENSTEIN M, HEDGES L V, HIGGINS J P T, et al. Meta分析导论[M]. 李国春, 吴勉华, 余小金 . 主译. 北京: 科学出版社, 2013. [本文引用:1]
[15] HEDGES L V, OLKIN I. Statistical methods for meta-analysis[M]. New York: Academic Press, 1985: 47-74. [本文引用:1]
[16] RIKKE B A, WYNES M W, ROZEBOOM L M, et al. Independent validation test of the vote-counting strategy used to rank biomarkers from published studies[J]. Biomark Med, 2015, 9(8): 751-761. [本文引用:1]