误差条形图可以辅助地反映统计推断的结论, 但两者并不总是等价的。欲比较两组的均值是否相等时, 误差条形图是否重叠并不等价于两组独立样本t检验的P值是否小于0.05。

研究者时常错误地解读误差条形图与组间对比（假设检验）之间的关系。国外一项研究纳入了473名作者在重要期刊发表的文章^[2], 该研究表明31.5%的作者错误地认为两组间的均值误差条形图（包括均值标准误、95%置信区间）不重叠等价于两组的均值有显著性差异（P< 0.05）。可见, 作者未加特别解释的误差条形图展示可能会让读者产生误解。

下文将用模拟研究和实例数据展示, 两组之间对比时不宜用误差条形图取代两独立样本t检验。

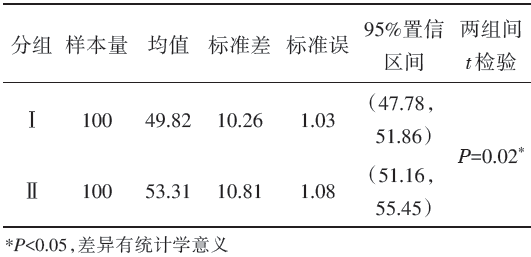
模拟一：随机产生两组样本量各为500且服从正态分布的数据集。第1组的均值为50, 标准差为10; 第2组的均值为52.5, 标准差为10。从第1组随机抽取100个数值作为样本Ⅰ , 从第2组随机抽取100个数值作为样本Ⅱ 。

欲比较样本Ⅰ 、Ⅱ 所来自总体的均值是否有差异, 采用两独立样本t检验, 结果为P< 0.05（表1）, 提示两样本代表的总体均值存在显著性差异。从样本Ⅰ 、Ⅱ 的误差条形图（图1）中可以看出：① 样本Ⅰ 、Ⅱ 的x ± SD误差条形图的上边界与下边界重叠; ② 样本Ⅰ 、Ⅱ 的\(\overline{x}\) ± SE的误差条形图的上边界与下边界未重叠; ③ 样本Ⅰ 、Ⅱ 的均值的95%置信区间有重叠。从模拟一可见, 当两独立样本t检验的P值小于0.05时, 误差条形图并不都是分离的。其中, 两样本的[x± SD]误差条形图、均值的95%置信区间都重叠。说明这两类误差条形图分离不是两组间t检验的P< 0.05的必要条件。所以, 对这两类的误差条形图而言, “ 两组间的均值误差条形图未重叠等价于两组的均值有显著性差异（P< 0.05）” 这一观点显然是错误的。该观点对于\(\overline{x}\)± SE的误差条形图是否成立?本文用模拟二的例子来证明。

表1

表1

表1 样本Ⅰ 、Ⅱ 的基本信息

表1 样本Ⅰ 、Ⅱ 的基本信息

图1

	Figure Option ViewDownloadNew Window
	图1 样本Ⅰ 、Ⅱ 的三类常用误差条形图

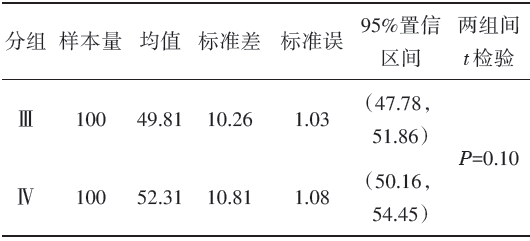
模拟二：随机产生两组样本量各为500且服从正态分布的数据集。第1组均值为50, 标准差为10; 第2组均值为51.5, 标准差为10。从第1组随机抽取100个数值作为样本Ⅲ , 从第2组随机抽取100个数值作为样本Ⅳ 。

欲比较样本Ⅲ 、Ⅳ 所来自总体的均值是否有差异, 采用两独立样本t检验, 结果为P> 0.05（表2）, 提示两样本代表的总体均值不存在显著性差异。但样本Ⅲ 与样本Ⅳ 的\(\overline{x}\)± SE误差条形图的上下边界不重叠（图2）。据此, 两样本的\(\overline{x}\)± SE误差条形图分离并不是两组间t检验得到P< 0.05的充分条件。所以, 对\(\overline{x}\)± SE的误差条形图而言, “ 两组间的均值误差条形图未重叠等价于两组的均值有显著性差异（P< 0.05）” 这一观点也是错误的。

表2

表2

表2 样本Ⅲ 、Ⅳ 的基本信息

表2 样本Ⅲ 、Ⅳ 的基本信息

综合上述模拟一与模拟二的误差条形图可见：① 模拟一、二中[x± SD]误差条形图的上边界与下边界均重叠; ② 模拟一、二中[x± SE]误差条形图的上边界与下边界均未重叠; ③ 模拟一、二中均值的95%置信区间均重叠。但模拟一的两组间t检验P< 0.05, 而模拟二的两组间t检验P> 0.05。说明当两样本的某一类型误差条形图重叠（或者未重叠）时, 对应假设检验的结果可能是P< 0.05, 也可能是P> 0.05。所以, 两组误差条形图是否重叠不宜直接取代两独立样本t检验是否显著。

在常用的误差条形图中, 置信区间常被用于提供组间对比（假设检验）的信息。本文用下面的实例来展现95%置信区间是否重叠与两独立样本t检验所得推论的关系。

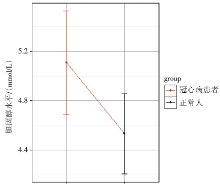
某医生收集了25例正常人与25例冠心病患者的胆固醇（mmol/L）观察值, 原始数据见表3^[5]。现欲比较正常人与冠心病患者的胆固醇平均水平有无差别。

表3

表3

表3 观察25 例正常人与25 例冠心病患者的胆固醇水平

表3 观察25 例正常人与25 例冠心病患者的胆固醇水平

该数据可以用两独立样本t检验进行组间比较, 结果为t=-2.25, P=0.03< 0.05, 说明正常人和冠心病患者的胆固醇均值差异有统计学意义。但从图3可看出, 正常人和冠心病患者胆固醇水平的95%置信区间有一定重叠。从该实例数据中可知两样本的95%置信区间重叠时, 两组的均值也可能存在显著性差异（此例属于模拟一述及的情况）。

图2

	Figure Option ViewDownloadNew Window
	图2 样本Ⅲ 、Ⅳ 的三类常用误差条形图

图3

	Figure Option ViewDownloadNew Window
	图3 正常人与冠心病患者的胆固醇水平及95%置信区间

为了强调试图通过误差条形图重叠与否便得出统计推断的对比结论是不妥的, 本文着重论述了“ 误差条形图是否分离等价于假设检验的P值是否小于显著性水平[α ]” 的矛盾之处。然而, 误差条形图与假设检验的结果有时确是一致的。例如, 本文提到两样本的[\(\overline{x}\)± SD]误差条形图、95%置信区间分离都不是两组间t检验的P< 0.05的必要条件, 需要注意的是这两类误差条形图分离是两组间t检验的P< 0.05的充分条件, 所以这两类的误差条形图不重叠时, 两组间t检验的P< 0.05。

为了避免出现错误的推论, 请注意以下几点：① 比较两样本均值是否有统计学差异, 应以假设检验（如t检验）的结果为准, 辅以误差条形图呈现两样本直观的差异。② 基于两组数据加工出的误差条形图重叠（或者分离）一定程度的时候, 确实会等价于组间对比的统计学结论。例如, 两独立样本的样本量均大于10且为均衡设计时, 两组均值的95%置信区间的误差条形图重叠小于1/4时, 则有假设检验的P< 0.05^{[6, 7]}。在实际应用时, 为了保证研究报告的可读性, 不建议利用这种等价性试图用误差条形图代替统计学检验（或反之）。