作者简介: 高永祥(1993-),男,山东潍坊人,硕士研究生,从事统计学方法及其医学应用研究。
Logistic 回归是一种广泛使用的统计模型。在实际应用中,有很多研究者往往忽视Logistic回归对样本量的要求,或者凭“纳入的研究对象人数充分”草草带过样本量问题,这些做法使主要影响因素与结局间关系的探索未能结合研究设计阶段对两类错误的设定。本文介绍三种Logistic回归样本量计算方法,并辅以实例说明,帮助研究者合理完成研究的设计与实施。
Logistic regression is a widely used statistical model. In practice, many researchers tend to ignore the requirements of the logistic regression on sample size or take over the sample size due to “enough subjects were included in the study populaton”, which fails to explore the relationship between the primary outcome and main impact indicator and ignores two types of errors. This paper introduced three Logistic regression sample size calculation methods, supplemented by examples to help researchers reasonably complete the design and implementation of the study.
Logistic 回归(logistic regression)模型被广泛应用于各学科领域, 如医学、社会科学、机器学习等, 主要适用于因变量是分类变量的情况, 尤其当因变量属于0-1变量。该模型采用的参数估计方法是极大似然估计(maximum likelihood estimate, MLE), 这就需要足够的样本量来保证参数估计的准确性, 而样本量的估计又是常常困扰研究者的一个问题, 以下将汇总二分类Logistic回归分析中几种常用的样本量确定方法。
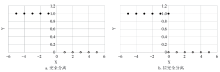
目前广泛使用的方法是EPV(events per variable)的方法, 即每个自变量的事件数, 其中事件表示因变量中个数较少的那一类[1]。例如调查胃癌发病与3种生活因素(X1代表不良饮食习惯, X2代表喜吃卤食和盐渍食物, X3代表精神状况)的关系[2], 若胃癌患者占的比例为20%, 那么当假设EPV=10时, 由于有3个协变量, 所以所需胃癌患者例数为10× 3=30, 总共需要的样本量(胃癌患者和健康对照)为30÷ 20%=150例。当EPV过少时, 容易出现分离(separation)现象。此现象出现在自变量若大于某个常数, 变量则仅与一个自变量相关联。例如当X为连续型变量时, 若X≤ 0时, 有Y恒为1, 则出现完全分离(complete separation)现象(见图1a), 此时参数估计无法收敛, 得不到回归系数的估计值。另一情形是, 当X< 0, Y恒为1, 但当X=0时Y兼有观察值0和1, 这时会出现拟完全分离(quasi-complete separation)现象(见图1b), 此时极大似然估计值异常大。统计学模拟研究表明[1], 在Logistic回归中推荐的经验准则是EPV 至少为10, 才能保证结果稳健。另外一个比较常用的经验准则是样本量为协变量个数的10~15倍[3]。具体应用时可以综合考虑两种经验准则。
Whittemore 1981年提出了罕见事件Logistic回归样本量估算公式[4], 随后Hsieh 对 Whittemore的公式进行了扩展[5], 在1998年提出了一个便于一般应用者实施的简单方法。建议借用样本均值比较和样本频率比较的样本含量计算公式来估算单因素Logistic回归所需的样本量, 再用方差膨胀因子对其修正便得到多因素Logistic回归所需的样本量[6]。
单因素Logistic回归中, 当X为连续型变量并且服从正态分布时, 样本量的计算公式为:
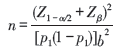
式(1)中p1为X取均值条件下Y = 1发生的频率, b为要度量的效应大小, 亦即X所对应回归系数的估计值。
当X为二分类变量时, 样本量的计算公式为:
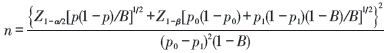
式(2)中p为总的阳性结局发生频率, B为X=1的个体在总观察人数中所占的比例(流行病学研究中对应于暴露比例), p0和p1分别为X=0和X=1时的阳性结局发生频率。
多因素Logistic回归样本量计算公式为:
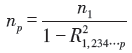
式(3)中的[R21, 234…p]就是以最主要的暴露因素X1为因变量, X2, ……, Xp 为自变量做线性回归得到的决定系数R2, n1为单因素Logistic 回归所需的样本量。其实, [1/(1-R21, 234…p)]被统计学家定义为一个重要参数— — 方差膨胀因子(variance inflation factor, VIF), 故多因素Logistic回归的样本量即为最主要的暴露因素所对应单因素Logistic回归所需的样本量n1乘以该因素对应的方差膨胀因子VIF。
实例1 某课题组拟探索非甾体抗炎药相关上消化道出血是否与吸烟之间存在关系, 现计算研究所需样本量。假设α =0.05(双侧), β =0.10(单侧)。
根据该课题组的回顾性分析, 已知B=0.48, p0 =0.43, p1=0.58, p=0.50, Z1-α /2 =1.96, Z1-β =1.28, 代入公式(2)可得n≈ 464。
实例2 假设在实例1中除了吸烟因素外, 还考虑饮酒、冠心病史、慢性胃炎史等可能影响上消化道出血的因素, 在这里我们最关心的暴露因素为是否吸烟, 并且已知吸烟与上述因素(自变量)之间的R2为0.07, 则根据公式(3)可得多因素Logistic回归所需样本量为n ≈ 499。
借助公式(1)~(3)进行手工计算, 麻烦且易出错。此处介绍如何利用开源软件R i386 3.2.1 和商业软件PASS11完成Logistic回归样本量的估算, R和PASS实际上也是基于前述公式实现的, 同样以实例1和实例2进行说明, 程序见表1和表2。R的计算结果, 实例1为464, 实例2约为499; PASS的计算结果, 实例1为463, 实例2为498。忽略计算精度, 二者结果基本类似。
| 表1 Logistic 回归样本量估算的R 程序及其说明 |
| 表2 Logistic 回归样本量估算的PASS 操作过程及说明 |
除了R软件、PASS可以用来计算样本量以外, 还有nQuery等软件可供读者使用, 在此不做详细说明, 周映雪等[7]具体介绍了用nQuery Advisor7.0实现Logistic回归样本量的计算以及提供了相应的SAS代码。不同的软件所采用的公式可能有一定差别, 因为统计学家针对Logistic回归样本量估算提出过不同的公式, 建议在样本量估算的文档中同时标注公式的出处。
EPV 通常被认为是Logistic回归模型中参数估计效果的主要决定因素, 在估算样本量时往往被格外重视。但是影响Logistic回归模型中参数估计效果的因素有很多, 比如因变量与自变量之间关系的强度、自变量之间的相关性(即共线性)等[8], van Smeden等认为对每个自变量EPV取10作为二分类Logistic回归样本量, 低估了合理的样本量水平, 建议通过Firth’ s校正予以改善[9]。Vittinghoff等也认为EPV 取10, 会致所得样本量偏低[10]。本文建议在采用经验法计算Logistic回归样本量时, 应同时兼顾所有自变量不同暴露水平下结局为阳性、阴性者的人数都足够多。
相较于经验法, 更提倡使用公式法来估算样本量, 并且建议使用影响面较大的权威软件包。本文介绍的两种软件各有利弊, 比如R免费, 而PASS则可提供更为详尽的输出。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|